Question

如图，△ABC是⊙O的内接三角形，BT为⊙O的切线，B为切点，P为AB上的一点，过点P作BC的平行线交直线BT于点E，交AC于点F
（I）当点P在线段AB上时，（如图1），求证：PA•PB=PE•PF；
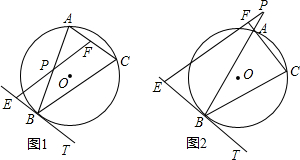
（II）当点P为线段BA的延长线上一点时（如图2），第（1）的结论还成立吗？如果成立请证明；如果不成立，请说明理由．

Answer 1

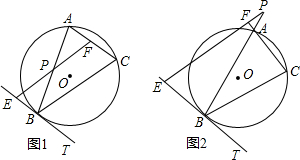
（Ⅰ）证明：如图1，∵EB为⊙O的切线，
∴∠ACB=∠ABE，
∵EF∥BC，
∴∠AFP=∠ACB，故∠AFP=∠ABE．
由于∠APF=∠EPB，∴△APF∽△BPE，
∴=，
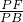∴PA•PB=PE•PF．

（Ⅱ）如图2，当点P在线段BA的延长线上时，（Ⅰ）的结论仍成立．
∵EB为⊙O的切线，
∴∠ACB=∠ABT，
∵EF∥BC，
∴∠ACB=∠ABT=∠AFP，
∴∠AFP=∠PBE．
再由∠BPE=∠FPA，可得△PAF∽△PEB，
∴=，
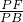∴PA•PB=PE•PF．
分析：（Ⅰ）利用圆周角、弦切角间的关系证明△APF∽△BPE，根据成比例线段证明 PA•PB=PE•PF 成立．
（Ⅱ）当点P在线段BA的延长线上时，（Ⅰ）的结论仍成立．先证明∠AFP=∠PBE，再由∠BPE=∠FPA，可得△PAF∽△PEB，根据成比例线段证明 PA•PB=PE•PF 成立．
点评：本题主要考查圆的相交弦及切线的性质，用三角形全等证明线段间的关系，体现了数形结合的数学思想，属于中档题．