��Ŀ����
����Ŀ��С����С����̽��ij����κ�������ʱ�����������¹��̣�
�������
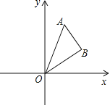
(1)��֪������![]() ������(-1,0),��
������(-1,0),��![]() = ����������Ϊ ���������߹��ڵ�(0,1�������ĶԳƵ������ߵı���ʽ�� .
= ����������Ϊ ���������߹��ڵ�(0,1�������ĶԳƵ������ߵı���ʽ�� .
�������
���Ƕ��壺����������![]() ,��
,��![]() ���ϵĵ�
���ϵĵ�![]() Ϊ���ģ����������߹���
Ϊ���ģ����������߹���
��![]() �ԳƵ�������
�ԳƵ�������![]() ,�������ֳ�������
,�������ֳ�������![]() Ϊ������
������![]() ��������������������
��������������������![]() ������������.
������������.
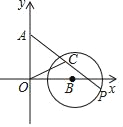
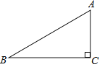
(2)��֪������![]() ���ڵ�
���ڵ�![]() ������������Ϊ
������������Ϊ![]() �����������������н��㣬��
�����������������н��㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
������
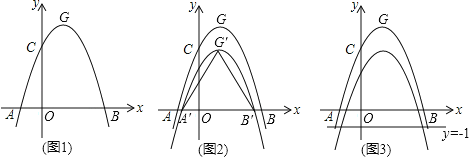
(3) ��֪������![]()
����������![]() ������������Ϊ
������������Ϊ![]() ,�����������������㣬��ǡ�������ǵĶ��㣬��
,�����������������㣬��ǡ�������ǵĶ��㣬��![]() ��ֵ���������ĵ����ꣻ
��ֵ���������ĵ����ꣻ
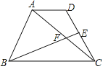
����������![]() ���ڵ�
���ڵ�![]() ������������Ϊ
������������Ϊ![]() ,�䶥��Ϊ
,�䶥��Ϊ![]() �����ڵ�
�����ڵ�![]() ������������Ϊ
������������Ϊ![]() ���䶥��Ϊ
���䶥��Ϊ![]() ���������ڵ�
���������ڵ�![]() ������������Ϊ
������������Ϊ![]() ���䶥��Ϊ
���䶥��Ϊ![]() ����(
����(![]() Ϊ
Ϊ
������).��![]() �ij�(�ú�
�ij�(�ú�![]() ��ʽ�ӱ�ʾ).
��ʽ�ӱ�ʾ).

���𰸡�������飺 ![]() ������������(-2,1)��
������������(-2,1)��![]() ���������
���������![]() ������������
������������![]() ����0��6������
����0��6������![]()
��������(1)��(-1��0)����![]() �����
����δ��![]() =-4��Ȼ��������߽���ʽ��Ϊ����ʽ������������ߵĶ������꣬�̶��ɵö�����ڣ�0��1���ĶԳƵ㣬�Ӷ���д��ԭ�����߹��ڵ�(0��1�������ĶԳƵ������ߵı���ʽ��
=-4��Ȼ��������߽���ʽ��Ϊ����ʽ������������ߵĶ������꣬�̶��ɵö�����ڣ�0��1���ĶԳƵ㣬�Ӷ���д��ԭ�����߹��ڵ�(0��1�������ĶԳƵ������ߵı���ʽ��
��2������������� ![]() �Ķ����ǣ�-1��6�����Ӷ���� (-1��6)����
�Ķ����ǣ�-1��6�����Ӷ���� (-1��6)����![]() �ĶԳƵ���
�ĶԳƵ���![]() ����
���� ![]() ���������������н��㣬����ȷ������
���������������н��㣬����ȷ������ ![]() �н⣬�̶����m��ȡֵ��Χ���ɣ�
�н⣬�̶����m��ȡֵ��Χ���ɣ�
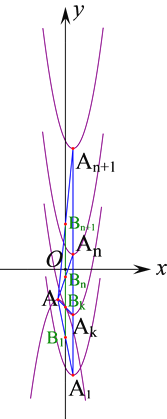
(3) �������������![]() �Լ�������
�Լ�������![]() ������������Ϊ
������������Ϊ![]() ���Ķ������꣬���������������������㣬��ǡ�������ǵĶ��㣬��
���Ķ������꣬���������������������㣬��ǡ�������ǵĶ��㣬��![]() ��ֵ���ٸ����е����깫ʽ��������������ĵ�������
��ֵ���ٸ����е����깫ʽ��������������ĵ�������
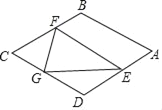
�� ��ͼ����![]() ��
��![]() ��
�� ![]() ��
��![]() ��
��![]() ��ֱ�����
��ֱ�����![]() ��
��![]() ��
�� ![]() ��
��![]() ����
����![]() ��
��![]() ����
���� ![]() ��
��![]() �ֱ����
�ֱ����![]() ��
��![]() ��
��![]() ��
��![]() ���ĶԳƣ���������ɵ�
���ĶԳƣ���������ɵ�![]() ��
��![]() ��
�� ![]() �ֱ��ǡ�
�ֱ��ǡ�![]() ��
��![]() ��
��![]() ����λ�ߣ��̶��ɵ�
����λ�ߣ��̶��ɵ�![]() ��
��![]() ����
���� ![]() ���ٸ��ݵ�����꼴�����
���ٸ��ݵ�����꼴�����![]() �ij�.
�ij�.
�������
(1)��(-1��0)����![]() ��
��![]() ��
��
��![]() ��
��
�ඥ��������(-2��1)��
��(-2��1)����(0��1)�ĶԳƵ���(2��1)��
������ĶԳƵ������߱���ʽ�ǣ�![]() ��
��
�� ![]() (��ͼ)
(��ͼ)

�������
(2) �� ![]() ��
��
�� �����ǣ�-1��6����
�� (-1��6)����![]() �ĶԳƵ���
�ĶԳƵ���![]() ��
��
�� ![]() ��
��
�� �������������
�� ![]() ���
���
�� ![]() ���
���
�� ![]() ��
��
�� ![]() ��(��ͼ)
��(��ͼ)
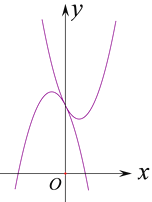
������
(3) �� ��![]() =
=![]() ��
��
�� ���㣨-1��![]() ����
����
���� ![]() �ã�
�ã�![]() ��
��
�� ![]() ��
��
�� ���㣨1��![]() ����
����
���� ![]() �ã�
�ã�![]() ��
��
�ɢ� �� �� ![]() ��
��
�� ![]() ��
��![]() ��
��
�� ![]() ��
��
�� ����������ֱ��ǣ�-1��0������1��12����
���е����깫ʽ���������������������ǣ�0��6����
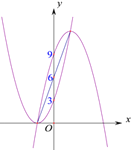
�� ��ͼ����![]() ��
��![]() ��
�� ![]() ��
��![]() ��
��![]() ��ֱ�����
��ֱ�����![]() ��
��![]() ��
�� ![]() ��
��![]() ��
��
��![]() ��
��![]() ����
���� ![]() ��
��![]() �ֱ����
�ֱ����![]() ��
��![]() ��
��![]() ��
��![]() ���ĶԳ���
���ĶԳ���
��![]() ��
��![]() ��
�� ![]() �ֱ��ǡ�
�ֱ��ǡ�![]() ��
��![]() ��
��![]() ����λ�ߣ�
����λ�ߣ�
��![]() ��
��![]() ����
���� ![]() ��
��
��![]() ��
�� ![]() ��
��
��![]()
![]() ]
]![]() .
.