题目内容
19.不等式组$\left\{\begin{array}{l}{3x+3>0}\\{-x≤-1}\end{array}\right.$的解集在数轴上表示为( )| A. |  | B. |  | C. |  | D. |  |
分析 先解两个不等式得到x>-1和x≥1,再根据同大取大确定不等式组的解集,然后利用数轴表示解集.
解答 解:$\left\{\begin{array}{l}{3x+3>0①}\\{-x≤-1②}\end{array}\right.$,
解①得x>-1,
解②得x≥1,
所以不等式组的解集为x≥1.
故选C.
点评 本题考查了一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
9.方程x2=64的解是( )
| A. | x=±8 | B. | x=8或x=-8 | C. | x=8 | D. | x=-8 |
9.若x1,x2是一元二次方程x2-3x-6=0的两个根,则x1+x2的值是( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
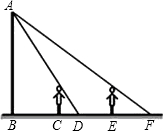 如图,李明晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知李明的身高是1.5米,则BC=3米.
如图,李明晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知李明的身高是1.5米,则BC=3米.