题目内容
已知△ABC≌△A′B′C′,A与A′,B与B′是对应顶点,△ABC的周长为12cm,AB=3cm,BC=4cm,则A′B′=________cm,B′C′=________cm,A′C′=________cm.
3 4 5
分析:由全等三角形的对应边相等可得出AB=A′B′,AC=A′C′,BC=B′C′,且周长相等,即可得到A′B′,B′C′及A′C′的长.
解答:∵△ABC≌△A′B′C′,
∴AB=A′B′=3cm,AC=A′C′,BC=B′C′=4cm,
∵△ABC的周长为12cm,∴△A′B′C′周长为12cm,
∴AC=A′C′=12-3-4=5cm.
故答案为:3;4;5.
点评:此题考查了全等三角形的性质,全等三角形的对应边相等,以及对应角相等,熟练掌握全等三角形的性质是解本题的关键.
分析:由全等三角形的对应边相等可得出AB=A′B′,AC=A′C′,BC=B′C′,且周长相等,即可得到A′B′,B′C′及A′C′的长.
解答:∵△ABC≌△A′B′C′,
∴AB=A′B′=3cm,AC=A′C′,BC=B′C′=4cm,
∵△ABC的周长为12cm,∴△A′B′C′周长为12cm,
∴AC=A′C′=12-3-4=5cm.
故答案为:3;4;5.
点评:此题考查了全等三角形的性质,全等三角形的对应边相等,以及对应角相等,熟练掌握全等三角形的性质是解本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知ABC的三边满足a2+b2+c2-ab-bc-ac=0,则这个三角形的形状是( )
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等边三角形 |
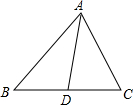 如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )
如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
已知△ABC中,cosA=
,tgB=1,则△ABC的形状是( )
| 1 |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
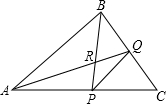 如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于
如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于