题目内容
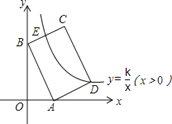
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 与
与![]() 轴交于点
轴交于点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 交反比例函数的图象于点
交反比例函数的图象于点![]() 交线段
交线段![]() 于点
于点![]() 连接
连接![]() .
.
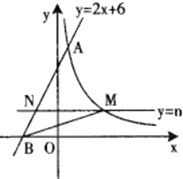
(1)求![]() 的值和反比例函数的表达式;
的值和反比例函数的表达式;
(2)当点![]() 是线段
是线段![]() 的中点时,求点
的中点时,求点![]() 的坐标;
的坐标;
(3)直线![]() 沿
沿![]() 轴方向平移,当
轴方向平移,当![]() 为何值时,
为何值时,![]() 的面积最大?
的面积最大?
【答案】(1)m=8;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 时,
时,![]() 的面积最大.
的面积最大.
【解析】
(1)求出点A的坐标,利用待定系数法即可解决问题;
(2)求出直线与x轴交点B的坐标,然后利用中点公式求解;
(3)根据三角形面积公式构建二次函数,利用二次函数的性质即可解决问题.
解:(1) ![]() 直线
直线![]() 经过点
经过点![]() ,
,
![]()
![]()
![]() 反比例函数经过点
反比例函数经过点![]()
![]()
![]()
![]() 反比例函数的解析式为
反比例函数的解析式为![]() ;
;
(2)当![]() 时,代入
时,代入![]()
则有:![]() 解得:
解得:![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
又![]() 点
点![]() 为A,B的中点,
为A,B的中点,
![]()
(3)由题意,点M,N的坐标为![]() ,
,
![]()
![]()
![]()
![]() 时,
时,![]() 的面积最大.
的面积最大.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
【题目】某学校为初三学生定制校服,对部分学生的服装型号做了调查,结果如下:
型号 | 140 | 150 | 160 | 170 | 180 |
男生 | 11 | 18 | 9 | 7 | 5 |
女生 | 9 | 12 | 18 | 7 | 4 |
下列说法正确的是( )
A.男生服装型号的众数大于女生服装型号的众数
B.男生服装型号的中位数等于女生服装型号的中位数
C.男生服装型号的众数小于女生服装型号的众数
D.男生服装型号的中位数大于女生服装型号的中位数