题目内容
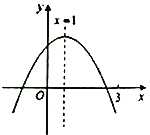
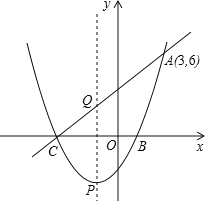
【题目】如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解,则t的取值范围是( )
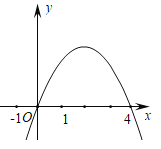
A.-5<t≤4 B.3<t≤4 C.-5<t<3 D.t>-5
【答案】B
【解析】
先利用抛物线的对称轴方程求出m得到抛物线解析式为y=-x2+4x,配方得到抛物线的顶点坐标为(2,4),再计算出当x=1或3时,y=3,结合函数图象,利用抛物线y=-x2+4x与直线y=t在1<x<3的范围内有公共点可确定t的范围.
∵ 抛物线y=-x2+mx的对称轴为直线x=2,
∴![]() ,
,
解之:m=4,
∴y=-x2+4x,
当x=2时,y=-4+8=4,
∴顶点坐标为(2,4),
∵ 关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解,
当x=1时,y=-1+4=3,
当x=2时,y=-4+8=4,
∴ 3<t≤4,
故选:B

练习册系列答案
相关题目
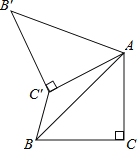
【题目】如图,直线![]() 和
和![]() 相交于点
相交于点![]() ,
,![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 是线段
是线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 的垂线交射线
的垂线交射线![]() 于点
于点![]() .
.
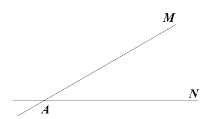
(1)确定点![]() 的位置,在线段
的位置,在线段![]() 上任取一点
上任取一点![]() ,根据题意,补全图形;
,根据题意,补全图形;
(2)设![]() cm,
cm,![]() cm,探究函数
cm,探究函数![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
①通过取点、画图、测量,得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
(要求:补全表格,相关数值保留一位小数)
②)建立平面直角坐标系![]() ,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;

③结合画出的函数图象,解决问题:当![]() 为
为![]() 斜边
斜边![]() 上的中线时,
上的中线时,![]() 的长度约为_____cm(结果保留一位小数).
的长度约为_____cm(结果保留一位小数).