题目内容
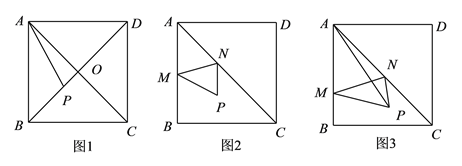
【题目】将正方形ABCD（如图1）作如下划分：第1次划分：分别连接正方形ABCD对边的中点（如图2），得线段HF和EG，它们交于点M，此时图2中共有5个正方形；第2次划分：将图2左上角正方形AEMH按上述方法再作划分，得图3，则图3中共有_________个正方形；若每次都把左上角的正方形依次划分下去，则第100次划分后，图中共有_______个正方形；继续划分下去，能否将正方形ABCD划分成有2011个正方形的图形？需说明理由.
【答案】9，401，不能理由见解析.
【解析】
本题需先根据图形，得出第2次划分共有多少个正方形，找出规律，得出n个的时候有多少个，从而得出结果．
∵第一次划分，得出5个正方形，
∴第2次划分，根据图形得出共有9个正方形；
∴依题意得：第n次划分后，图中共有4n+1个正方形
∴第100次划分后，共有401个正方形；
∵第n次划分后，图中共有4n+1个正方形，
∴方程4n+1=2011没有整数解，
∴不能得到2011个正方形.
练习册系列答案
相关题目
【题目】王小方开了一家服装店，专卖羽绒服，下表是去年一年各月的销售量情况：
月份 | 一 | 二 | 三 | 四 | 五 | 六 |
销售量/件 | 120 | 90 | 40 | 10 | 6 | 4 |
月份 | 七 | 八 | 九 | 十 | 十一 | 十二 |
销售量/件 | 3 | 5 | 3 | 120 | 80 | 120 |
(1)计算各季度的销售量，并用一幅合适的统计图表示；
(2)计算各季度的销售量在全年销售量中所占的百分比(精确到1%)，并用适当的统计图表示；
(3)用一幅合适的统计图表示各季度销售量的变化情况.
