题目内容
如图,由图1通过图形的变换可以得到图2.观察图形的变换方式,回答下列问题:

(1)请简述由图1变换为图2的过程:______________________________________.
(2)说明图2中四边形ECFD是正方形;
(3)若AD=3,DB=4,试求图2中△ADE和△BDF面积的和S.
(2)说明图2中四边形ECFD是正方形;
(3)若AD=3,DB=4,试求图2中△ADE和△BDF面积的和S.
(1)将△A′DF绕点D顺时针旋转90°得△ADE;
(2)∵∠DFB=90°,∴∠DFC=90°.
∵△ADE是由△A′DF绕点D顺时针旋转90°而得,
∴∠AED=90°,
∴∠DEC=90°.
又∵∠DFC=90°,∠C=90°,
∴四边形ECFD为矩形
又∵DE=DF,∴四边形ECFD为正方形;
(3)∵四边形ECFD为正方形,∴∠EDF=90°,∴∠ADE+∠BDF =90°.
又∵∠ADE=∠A′DF,∴∠A′DF+∠BDF =90°,即∠A′DB =90°,
∵A′D=AD,AD=3,∴A′D=3.
∴S=S△ADE+ S△BDF= S△A′DF+ S△BDF=S△A′DB= ×3×4=6.
×3×4=6.
(2)∵∠DFB=90°,∴∠DFC=90°.
∵△ADE是由△A′DF绕点D顺时针旋转90°而得,
∴∠AED=90°,
∴∠DEC=90°.
又∵∠DFC=90°,∠C=90°,
∴四边形ECFD为矩形
又∵DE=DF,∴四边形ECFD为正方形;
(3)∵四边形ECFD为正方形,∴∠EDF=90°,∴∠ADE+∠BDF =90°.
又∵∠ADE=∠A′DF,∴∠A′DF+∠BDF =90°,即∠A′DB =90°,
∵A′D=AD,AD=3,∴A′D=3.
∴S=S△ADE+ S△BDF= S△A′DF+ S△BDF=S△A′DB=
 ×3×4=6.
×3×4=6.
练习册系列答案
相关题目

 △ABC在平面直角坐标系中如图所示,
△ABC在平面直角坐标系中如图所示,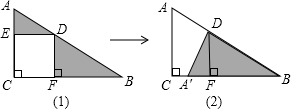 如图,由图1通过图形的变换可以得到图2.观察图形的变换方式,回答下列问题:
如图,由图1通过图形的变换可以得到图2.观察图形的变换方式,回答下列问题: 如图,由图1通过图形的变换可以得到图2.观察图形的变换方式,回答下列问题:
如图,由图1通过图形的变换可以得到图2.观察图形的变换方式,回答下列问题: