题目内容
 如图,由图1通过图形的变换可以得到图2.观察图形的变换方式,回答下列问题:
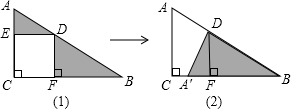
如图,由图1通过图形的变换可以得到图2.观察图形的变换方式,回答下列问题:(1)请简述由图1变换为图2的过程:
以A点为旋转中心,把△DAE绕点A逆时针旋转90°
以A点为旋转中心,把△DAE绕点A逆时针旋转90°
.(2)说明图2中四边形ECFD是正方形;
(3)若AD=3,DB=4,试求图2中△ADE和△BDF面积的和S.
分析:(1)由于图1通过图形的变换可以得到图2,则可把△DAE绕点A逆时针旋转90°得到△DA′F;
(2)根据旋转的性质得DE=DF,∠DEC=∠DFC=90°,而∠C=90°,可判断四边形ECFD是正方形;
(3)根据旋转的性质得到∠ADA′=90°,DA=DA′=3,再利用勾股定理计算出AB=5,利用等积法求出DF的长,然后根据勾股定理可计算出A′F=
,则BF=A′B-A′F=
,然后利用三角形面积公式计算.
(2)根据旋转的性质得DE=DF,∠DEC=∠DFC=90°,而∠C=90°,可判断四边形ECFD是正方形;
(3)根据旋转的性质得到∠ADA′=90°,DA=DA′=3,再利用勾股定理计算出AB=5,利用等积法求出DF的长,然后根据勾股定理可计算出A′F=
| 9 |
| 5 |
| 16 |
| 5 |
解答:解:(1)把△DAE绕点A逆时针旋转90°得到△DA′F,如图2;
(2)∵图1通过图形的变换可以得到图2,即把△DAE绕点A逆时针旋转90°得到△DA′F,
∴DE=DF,∠DEC=∠DFC=90°,
而∠C=90°,
∴四边形ECFD是正方形;
(3)∵把△DAE绕点A逆时针旋转90°得到△DA′F,
∵∠ADA′=90°,DA=DA′=3,
∴∠BDA′=90°,
∴A′B=
=
=5,
∴
DF•A′B=
DA′•DB,
∴DF=
,
在Rt△DA′F中,A′F=
=
,
∴S△DA′F=
×
×
=
,
∴S△ADE=
;
∵BF=A′B-A′F=
,
∴S△BDF=
×
×
=
.
故答案为以A点为旋转中心,把△DAE绕点A逆时针旋转90°.
(2)∵图1通过图形的变换可以得到图2,即把△DAE绕点A逆时针旋转90°得到△DA′F,
∴DE=DF,∠DEC=∠DFC=90°,
而∠C=90°,
∴四边形ECFD是正方形;
(3)∵把△DAE绕点A逆时针旋转90°得到△DA′F,
∵∠ADA′=90°,DA=DA′=3,
∴∠BDA′=90°,
∴A′B=
| DA′2+DB2 |
| 32+42 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=
| 12 |
| 5 |
在Rt△DA′F中,A′F=
32-(
|
| 9 |
| 5 |
∴S△DA′F=
| 1 |
| 2 |
| 9 |
| 5 |
| 12 |
| 5 |
| 54 |
| 25 |
∴S△ADE=
| 54 |
| 25 |
∵BF=A′B-A′F=
| 16 |
| 5 |
∴S△BDF=
| 1 |
| 2 |
| 16 |
| 5 |
| 12 |
| 5 |
| 96 |
| 25 |
故答案为以A点为旋转中心,把△DAE绕点A逆时针旋转90°.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正方形的判定方法以及勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 △ABC在平面直角坐标系中如图所示,
△ABC在平面直角坐标系中如图所示, 如图,由图1通过图形的变换可以得到图2.观察图形的变换方式,回答下列问题:
如图,由图1通过图形的变换可以得到图2.观察图形的变换方式,回答下列问题: