题目内容
 设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF.再以对角线AE为边作第三个正方形,如此下去…
设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF.再以对角线AE为边作第三个正方形,如此下去…(1)记正方形ABCD的边长为a1=1.按照上述方法所作的正方形边长依次记为a2,a3,a4,…,请写出a2,a3,a4的值;
(2)根据以上规律,请你写出用含字母n的代数式表示第n个正方形的边长.
分析:(1)求a2的长即AC的长,根据直角△ABC中AB2+BC2=AC2可以计算,同理计算a3、a4.
(2)由(1)知,a2=
a2…,an=
an-1可以找出第n个正方形边长的表达式.
(2)由(1)知,a2=
| 2 |
| 2 |
解答:解:(1)a2=AC,且在直角△ABC中,AB2+BC2=AC2,
∴a2=
a1=
,
同理a3=
a2=(
)a1=2,
a4=
a3=(
)3a1=2
;
(2)由(1)结论可知:
a2=
a1=
,
a3=
a2=(
)a1=2,
a4=
a3=(
)3a1=2
;
…
故找到规律
an=(
)n-1a1=(
)n-1.
∴a2=
| 2 |
| 2 |
同理a3=
| 2 |
| 2 |
a4=
| 2 |
| 2 |
| 2 |
(2)由(1)结论可知:
a2=
| 2 |
| 2 |
a3=
| 2 |
| 2 |
a4=
| 2 |
| 2 |
| 2 |
…
故找到规律
an=(
| 2 |
| 2 |
点评:本题考查了勾股定理在直角三角形中的运用,考查了学生找规律的能力,本题中找到an的规律是解题的关键.

练习册系列答案
相关题目
 方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去….
方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…. 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a101=
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a101= 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边长作第2个正方形ACEF,再以第2个正方形ACEF的对角线AE为边长作第3个正方形,如此进行下去,…
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边长作第2个正方形ACEF,再以第2个正方形ACEF的对角线AE为边长作第3个正方形,如此进行下去,…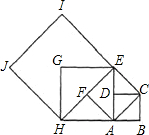 阅读下面的文字,回答后面的问题.
阅读下面的文字,回答后面的问题.