题目内容
若| x |
| x2+x+1 |
| x2 |
| x4+x2+1 |
分析:先将
化简为含有
的形式,然后代入进行求值.
| x2 |
| x4+x2+1 |
| x |
| x2+x+1 |
解答:解:
=
=(
)(
)
=
•
,把
=a代入得:
a×
=
.
故答案为:
.
| x2 |
| x4+x2+1 |
| x2 |
| (x2+x+1)(x2-x+1) |
=(
| x |
| x2+x+1 |
| x |
| (x2+x+1)-2x |
=
| x |
| x2+x+1 |
| 1 | ||
|
| x |
| x2+x+1 |
a×
| 1 | ||
|
| a2 |
| 1-2a |
故答案为:
| a2 |
| 1-2a |
点评:本题考查了分式的化简求值,难度适中,关键是把所求分式化简成含有
的形式,然后根据条件求解.
| x |
| x2+x+1 |

练习册系列答案
相关题目
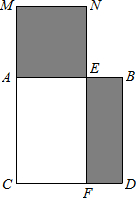 如图,已知线段AB的长为1,以AB为边在AB下方作正方形ACDB.取AB边上一点E,以AE为边在AB的上方作正方形AENM.过E作EF⊥CD,垂足为F点.若正方形AENM与四边形EFDB的面积相等,设AE=x,可列方程为
如图,已知线段AB的长为1,以AB为边在AB下方作正方形ACDB.取AB边上一点E,以AE为边在AB的上方作正方形AENM.过E作EF⊥CD,垂足为F点.若正方形AENM与四边形EFDB的面积相等,设AE=x,可列方程为