题目内容
抛物线y=mx2-5mx+n与y轴正半轴交于点C,与x轴分别交于点A和点B(1,0),且OC2=OA•OB.
(1)求抛物线的解析式;
(2)点P是y轴上一点,当△PBC和△ABC相似时,求点P的坐标.
解:(1)由题意,得抛物线对称轴是直线 ,
,
∵点A和点B关于直线 对称,点B(1,0),
对称,点B(1,0),
∴A(4,0),
∵OC2=OA•OB=4×1=4,
∴OC=2,
∵点C在y轴正半轴上,
∴C(0,2),
∴ ;
;
(2)由题意,可得AB=3, ,
,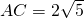 ,
,
∵OC2=OA•OB,
∴ ,
,
又∠BOC=∠COA,
∴△BOC∽△COA,
∴∠OCB=∠OAC,
∴△PBC和△ABC相似时,分下列两种情况:
①当 时,得
时,得 ,∴
,∴ ,
,
∴ ,
,
∴ ;
;
②当 时,得
时,得 ,∴
,∴ ,
,
∴ ,
,
∴ ,
,
综合①、②当△PBC和△ABC相似时 或
或 .
.
分析:(1)由题意,得抛物线对称轴是直线 ,并且A和B关于直线
,并且A和B关于直线 对称,因为点B(1,0),所以A(4,0),又因为OC2=OA•OB,进而求出OC的长,所以C点的坐标可求,从而求出抛物线的解析式;
对称,因为点B(1,0),所以A(4,0),又因为OC2=OA•OB,进而求出OC的长,所以C点的坐标可求,从而求出抛物线的解析式;
(2)首先△BOC∽△COA,所以∠OCB=∠OAC,所以当△PBC和△ABC相似时,分两种情况①当 时②当
时②当 时分别求出符合题意的OP的长,即可求出P点的坐标.
时分别求出符合题意的OP的长,即可求出P点的坐标.
点评:本题考查了求二次函数的解析式、相似三角形的判定和性质,解题的关键是要注意分类讨论的数学思想运用,防止漏解.
 ,
,∵点A和点B关于直线
 对称,点B(1,0),
对称,点B(1,0),∴A(4,0),
∵OC2=OA•OB=4×1=4,
∴OC=2,
∵点C在y轴正半轴上,
∴C(0,2),
∴
 ;
;(2)由题意,可得AB=3,
 ,
,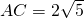 ,
,∵OC2=OA•OB,
∴
 ,
,又∠BOC=∠COA,
∴△BOC∽△COA,
∴∠OCB=∠OAC,
∴△PBC和△ABC相似时,分下列两种情况:
①当
 时,得
时,得 ,∴
,∴ ,
,∴
 ,
,∴
 ;
;②当
 时,得
时,得 ,∴
,∴ ,
,∴
 ,
,∴
 ,
,综合①、②当△PBC和△ABC相似时
 或
或 .
.分析:(1)由题意,得抛物线对称轴是直线
 ,并且A和B关于直线
,并且A和B关于直线 对称,因为点B(1,0),所以A(4,0),又因为OC2=OA•OB,进而求出OC的长,所以C点的坐标可求,从而求出抛物线的解析式;
对称,因为点B(1,0),所以A(4,0),又因为OC2=OA•OB,进而求出OC的长,所以C点的坐标可求,从而求出抛物线的解析式; (2)首先△BOC∽△COA,所以∠OCB=∠OAC,所以当△PBC和△ABC相似时,分两种情况①当
 时②当
时②当 时分别求出符合题意的OP的长,即可求出P点的坐标.
时分别求出符合题意的OP的长,即可求出P点的坐标.点评:本题考查了求二次函数的解析式、相似三角形的判定和性质,解题的关键是要注意分类讨论的数学思想运用,防止漏解.

练习册系列答案
相关题目
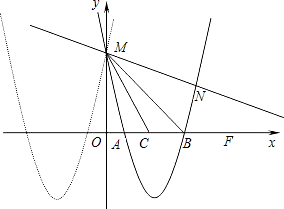 如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B.
如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B. (2012•顺义区一模)如图,在平面直角坐标系xOy中,抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3),
(2012•顺义区一模)如图,在平面直角坐标系xOy中,抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3),