题目内容
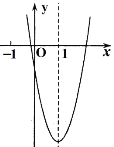
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
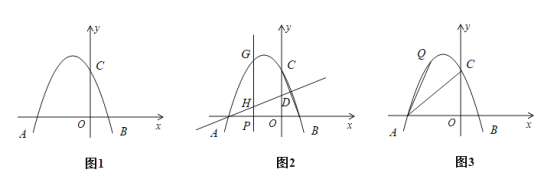
(1)求抛物线的解析式.
(2)如图2,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 点是
点是![]() 轴上一个动点,过点
轴上一个动点,过点![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,当点
,当点![]() 、
、![]() 、
、![]() 、
、![]() 四个点组成的四边形是平行四边形时,求此时
四个点组成的四边形是平行四边形时,求此时![]() 点坐标.
点坐标.
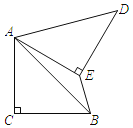
(3)如图3,连接![]() 和
和![]() ,
,![]() 点是抛物线上一个动点,连接
点是抛物线上一个动点,连接![]() ,当
,当![]() 时,求
时,求![]() 点的坐标.
点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,
,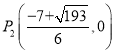 ,
, ;(3)
;(3)![]() ,
,![]() .
.
【解析】
(1)把A、B、C三点坐标分别代入函数解析式得到三元一次方程组,解方程组即可;
(2)设![]() ,则
,则![]() ,
,![]() ,根据
,根据![]() 轴,可表示出GH的长,根据平行四边形的性质列方程解答即可;
轴,可表示出GH的长,根据平行四边形的性质列方程解答即可;
(3)分两种情况讨论:①![]() 在
在![]() 上方,证
上方,证![]() ②
②![]() 在
在![]() 下方,设
下方,设![]() 和
和![]() 轴交于点
轴交于点![]() ,过
,过![]() 作
作![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,证
,证![]()
(1)将![]() 、
、![]() 、
、![]() 分别代入y=ax2+bx+c,得:
分别代入y=ax2+bx+c,得:
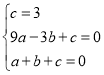 ,
,
解得![]() ,
,![]() ,
,![]()
∴![]()
(2)设![]() 则
则![]() ,
,![]()
∵![]() 轴
轴
∴![]()
∵四个点![]() 、
、![]() 、
、![]() 、
、![]() 组成平行四边形
组成平行四边形
∴![]()
∴![]()
解得:![]() ,
,![]() ,
,![]()
∴![]() ,
,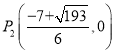 ,
,
(3)①![]() 在
在![]() 上方,如图所示,过
上方,如图所示,过![]() 作
作![]() ,交
,交![]() 于
于![]()
证明![]()
∵![]()
∴![]()
∴![]()
∴![]() ,此时
,此时![]() 在抛物线上,
在抛物线上,
∴![]()

②![]() 在
在![]() 下方
下方
![]() 和
和![]() 轴交于点
轴交于点![]() ,过
,过![]() 作
作![]() ,过
,过![]() 作
作![]() 轴于
轴于![]()
证明![]()
∵![]()
∴![]()
∴![]()
设![]() ,则
,则![]()
∴![]()
∴![]() ,解得
,解得![]()
∴![]()
∴![]() 表达式:
表达式:![]()
联立: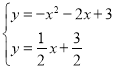 ,解得
,解得![]() 或
或![]() (舍)
(舍)
∴![]()


练习册系列答案
相关题目