题目内容
已知:
12=1=
12+22=
12+22+32=
观察上面算式的规律并解答下列各题:
(1)12+22+3+42=
(2)12+22+3+42+…+n2=
(3)计算:12+22+32+42+…+1002的值.
12=1=
| 1×(1+1)×(2×1+1) |
| 6 |
12+22=
| 2×(2+1)×(2×2+1) |
| 6 |
12+22+32=
| 3×(3+1)×(2×3+1) |
| 6 |
观察上面算式的规律并解答下列各题:
(1)12+22+3+42=
| ( )×( )×( ) |
| 6 |
(2)12+22+3+42+…+n2=
| ( )×( )×( ) |
| 6 |
(3)计算:12+22+32+42+…+1002的值.
考点:规律型:数字的变化类
专题:
分析:由上面算式可以得出如下规律,12+22+32+42+…+n2=
,由此规律计算即可.
| n(n+1)(n+2) |
| 6 |
解答:解:(1)12+22+3+42=
=30;
(2)12+22+3+42+…+n2=
;
(3)12+22+32+42+…+1002
=
=338350.
| 4×(4+1)(4×2+1) |
| 6 |
(2)12+22+3+42+…+n2=
| n(n+1)(n+2) |
| 6 |
(3)12+22+32+42+…+1002
=
| 100×(100+1)×(100×2+1) |
| 6 |
=338350.
点评:此题考查算式的计算规律,注意从简单的情形入手,找出规律,解决问题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
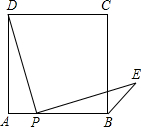 点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得到线段PE,连接BE,则∠CBE等于
点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得到线段PE,连接BE,则∠CBE等于 如图,OA表示
如图,OA表示