Question

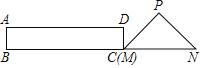
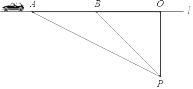
【题目】均衡化验收以来，乐陵每个学校都高楼林立，校园环境美如画，软件、硬件等设施齐全，小明想要测量学校食堂和食堂正前方一棵树的高度，他从食堂楼底M处出发，向前走6 米到达A处，测得树顶端E的仰角为30°，他又继续走下台阶到达C处，测得树的顶端的仰角是60°，再继续向前走到大树底D处，测得食堂楼顶N的仰角为45°，已如A点离地面的高度AB＝4米，∠BCA＝30°，且B、C、D 三点在同一直线上．

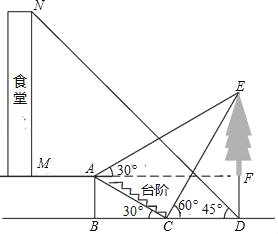
（1）求树DE的高度；

（2）求食堂MN的高度．

Answer 1

【答案】（1）12米；（2）（2+8）米

【解析】

（1）设DE＝x，先证明△ACE是直角三角形，∠CAE＝60°，∠AEC＝30°，得到AE＝16，根据EF=8求出x的值得到答案；

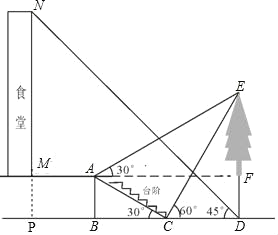
（2）延长NM交DB延长线于点P，先分别求出PB、CD得到PD，利用∠NDP＝45°得到NP，即可求出MN.

（1）如图，设DE＝x，

∵AB＝DF＝4，∠ACB＝30°，

∴AC＝8，

∵∠ECD＝60°，

∴△ACE是直角三角形，

∵AF∥BD，

∴∠CAF＝30°，

∴∠CAE＝60°，∠AEC＝30°，

∴AE＝16，

∴Rt△AEF中，EF＝8，

即x﹣4＝8，

解得x＝12，

∴树DE的高度为12米；

（2）延长NM交DB延长线于点P，则AM＝BP＝6，

由（1）知CD＝CE＝×AC＝4，BC＝4，

∴PD＝BP+BC+CD＝6+4+4＝6+8，

∵∠NDP＝45°，且∠NPD＝90°，

∴NP＝PD＝6+8，

∴NM＝NP﹣MP＝6+8﹣4＝2+8，

∴食堂MN的高度为（2+8）米．