题目内容
 如图,已知A1(1,0)、C(0,1),以A1C为一边向外作长宽比为
如图,已知A1(1,0)、C(0,1),以A1C为一边向外作长宽比为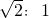 的矩形,再以A2B1为一边向外作长宽比为
的矩形,再以A2B1为一边向外作长宽比为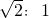 的矩形,以此类推,求:
的矩形,以此类推,求:
(1)点B1的坐标______,S△A1A2B2=______;
(2)求S△A1A2B2+S△A2A3B3+…+S△AnAn+1Bn+1=______.
解:(1)∵A1(1,0)、C(0,1),
 ∴OA1=OC=1,
∴OA1=OC=1,
∵∠A1OC=90°,
∴A1C= =
= ,∠OA1C=∠OCA1=45°,
,∠OA1C=∠OCA1=45°,
∵以A1C为一边向外作长宽比为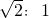 的矩形,
的矩形,
∴A1B1= A1C=2,∠B1A1A2=180°-90°-45°=45°,
A1C=2,∠B1A1A2=180°-90°-45°=45°,
∴△A1A2B1是等腰直角三角形,
∴A1A2= A1B1=2
A1B1=2 .
.
如图,作三角形A1A2B1的高B1D,则A1D=B1D= A1A2=
A1A2= ,
,
∴OD=OA1+A1D=1+ ,
,
∴点B1的坐标为(1+ ,
, );
);
过点B2作B2E⊥x轴于点E,
易证三角形A2A3B2是等腰直角三角形,
∵A2B1=A1B1=2,
∴A2B2= A2B1=2
A2B1=2 ,
,
∴A2A3= A2B2=4,
A2B2=4,
∴B2E= A2A3=2,
A2A3=2,
∴S△A1A2B2= A1A2•B2E=
A1A2•B2E= ×2
×2 ×2=2
×2=2 ;
;
 (2)过点B3作B3F⊥x轴于点F,
(2)过点B3作B3F⊥x轴于点F,
易证三角形A3A4B3是等腰直角三角形,
∵A3B2=A2B2=2 ,
,
∴A3B3= A3B2=4,
A3B2=4,
∴A3A4= A3B3=4
A3B3=4 ,
,
∴B3F= A3A4=2
A3A4=2 ,
,
∴S△A2A3B3= A2A3•B3F=
A2A3•B3F= ×4×2
×4×2 =4
=4 ;
;
同理,可得S△A3A4B4= ×4
×4 ×4=8
×4=8 ;
;
…
S△AnAn+1Bn+1=2n ;
;
∴S△A1A2B2+S△A2A3B3+…+S△AnAn+1Bn+1=2 +4
+4 +8
+8 +…+2n
+…+2n =
= (2+4+8+…+2n)=
(2+4+8+…+2n)= ×
×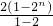 =(2n+1-2)
=(2n+1-2) .
.
故答案为(1+ ,
, ),2
),2 ;(2n+1-2)
;(2n+1-2) .
.
分析:(1)先由勾股定理求出A1C= ,则A1B1=2,再作等腰直角三角形A1A2B1斜边上的高B1D,根据等腰直角三角形的性质求出A1D和B1D的长,进而得到点B1的坐标;过点B2作B2E⊥x轴于点E,由于三角形A2A3B2是等腰直角三角形,则B2E=
,则A1B1=2,再作等腰直角三角形A1A2B1斜边上的高B1D,根据等腰直角三角形的性质求出A1D和B1D的长,进而得到点B1的坐标;过点B2作B2E⊥x轴于点E,由于三角形A2A3B2是等腰直角三角形,则B2E= A2A3,然后根据三角形的面积公式即可求出S△A1A2B2;
A2A3,然后根据三角形的面积公式即可求出S△A1A2B2;
(2)过点B3作B3F⊥x轴于点F,易证三角形A3A4B3是等腰直角三角形,则B3F= A3A4=2
A3A4=2 ,又A2A3=4,根据三角形的面积公式求出S△A2A3B3=
,又A2A3=4,根据三角形的面积公式求出S△A2A3B3= A2A3•B3F=4
A2A3•B3F=4 ;同理求出S△A3A4B4=
;同理求出S△A3A4B4= ×4
×4 ×4=8
×4=8 ;…;S△AnAn+1Bn+1=2n
;…;S△AnAn+1Bn+1=2n ;然后根据等比数列的求和公式即可求解.
;然后根据等比数列的求和公式即可求解.
点评:本题考查了矩形的性质,等腰直角三角形的判定与性质,相似三角形的判定与性质,三角形的面积,等比数列的求和,综合性较强,有一定难度.
 ∴OA1=OC=1,
∴OA1=OC=1,∵∠A1OC=90°,
∴A1C=
 =
= ,∠OA1C=∠OCA1=45°,
,∠OA1C=∠OCA1=45°,∵以A1C为一边向外作长宽比为
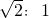 的矩形,
的矩形,∴A1B1=
 A1C=2,∠B1A1A2=180°-90°-45°=45°,
A1C=2,∠B1A1A2=180°-90°-45°=45°,∴△A1A2B1是等腰直角三角形,
∴A1A2=
 A1B1=2
A1B1=2 .
.如图,作三角形A1A2B1的高B1D,则A1D=B1D=
 A1A2=
A1A2= ,
,∴OD=OA1+A1D=1+
 ,
,∴点B1的坐标为(1+
 ,
, );
);过点B2作B2E⊥x轴于点E,
易证三角形A2A3B2是等腰直角三角形,
∵A2B1=A1B1=2,
∴A2B2=
 A2B1=2
A2B1=2 ,
,∴A2A3=
 A2B2=4,
A2B2=4,∴B2E=
 A2A3=2,
A2A3=2,∴S△A1A2B2=
 A1A2•B2E=
A1A2•B2E= ×2
×2 ×2=2
×2=2 ;
; (2)过点B3作B3F⊥x轴于点F,
(2)过点B3作B3F⊥x轴于点F,易证三角形A3A4B3是等腰直角三角形,
∵A3B2=A2B2=2
 ,
,∴A3B3=
 A3B2=4,
A3B2=4,∴A3A4=
 A3B3=4
A3B3=4 ,
,∴B3F=
 A3A4=2
A3A4=2 ,
,∴S△A2A3B3=
 A2A3•B3F=
A2A3•B3F= ×4×2
×4×2 =4
=4 ;
;同理,可得S△A3A4B4=
 ×4
×4 ×4=8
×4=8 ;
;…
S△AnAn+1Bn+1=2n
 ;
;∴S△A1A2B2+S△A2A3B3+…+S△AnAn+1Bn+1=2
 +4
+4 +8
+8 +…+2n
+…+2n =
= (2+4+8+…+2n)=
(2+4+8+…+2n)= ×
×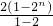 =(2n+1-2)
=(2n+1-2) .
.故答案为(1+
 ,
, ),2
),2 ;(2n+1-2)
;(2n+1-2) .
.分析:(1)先由勾股定理求出A1C=
 ,则A1B1=2,再作等腰直角三角形A1A2B1斜边上的高B1D,根据等腰直角三角形的性质求出A1D和B1D的长,进而得到点B1的坐标;过点B2作B2E⊥x轴于点E,由于三角形A2A3B2是等腰直角三角形,则B2E=
,则A1B1=2,再作等腰直角三角形A1A2B1斜边上的高B1D,根据等腰直角三角形的性质求出A1D和B1D的长,进而得到点B1的坐标;过点B2作B2E⊥x轴于点E,由于三角形A2A3B2是等腰直角三角形,则B2E= A2A3,然后根据三角形的面积公式即可求出S△A1A2B2;
A2A3,然后根据三角形的面积公式即可求出S△A1A2B2;(2)过点B3作B3F⊥x轴于点F,易证三角形A3A4B3是等腰直角三角形,则B3F=
 A3A4=2
A3A4=2 ,又A2A3=4,根据三角形的面积公式求出S△A2A3B3=
,又A2A3=4,根据三角形的面积公式求出S△A2A3B3= A2A3•B3F=4
A2A3•B3F=4 ;同理求出S△A3A4B4=
;同理求出S△A3A4B4= ×4
×4 ×4=8
×4=8 ;…;S△AnAn+1Bn+1=2n
;…;S△AnAn+1Bn+1=2n ;然后根据等比数列的求和公式即可求解.
;然后根据等比数列的求和公式即可求解.点评:本题考查了矩形的性质,等腰直角三角形的判定与性质,相似三角形的判定与性质,三角形的面积,等比数列的求和,综合性较强,有一定难度.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图,已知A1(0,1),
如图,已知A1(0,1),
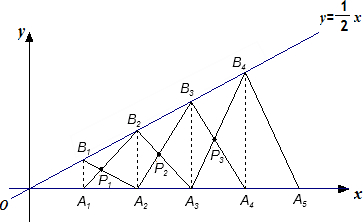
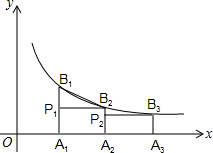 如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y=
如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y= 如图,已知A1(1,0)、C(0,1),以A1C为一边向外作长宽比为
如图,已知A1(1,0)、C(0,1),以A1C为一边向外作长宽比为