题目内容
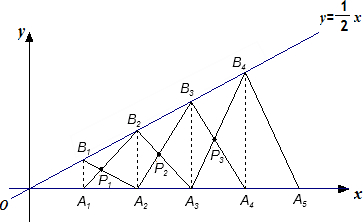
 如图,已知A1(1,0)、C(0,1),以A1C为一边向外作长宽比为
如图,已知A1(1,0)、C(0,1),以A1C为一边向外作长宽比为| 2 |
| 2 |
(1)点B1的坐标
(2)求S△A1A2B2+S△A2A3B3+…+S△AnAn+1Bn+1=
分析:(1)先由勾股定理求出A1C=
,则A1B1=2,再作等腰直角三角形A1A2B1斜边上的高B1D,根据等腰直角三角形的性质求出A1D和B1D的长,进而得到点B1的坐标;过点B2作B2E⊥x轴于点E,由于三角形A2A3B2是等腰直角三角形,则B2E=
A2A3,然后根据三角形的面积公式即可求出S△A1A2B2;
(2)过点B3作B3F⊥x轴于点F,易证三角形A3A4B3是等腰直角三角形,则B3F=
A3A4=2
,又A2A3=4,根据三角形的面积公式求出S△A2A3B3=
A2A3•B3F=4
;同理求出S△A3A4B4=
×4
×4=8
;…;S△AnAn+1Bn+1=2n
;然后根据等比数列的求和公式即可求解.
| 2 |
| 1 |
| 2 |
(2)过点B3作B3F⊥x轴于点F,易证三角形A3A4B3是等腰直角三角形,则B3F=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:(1)∵A1(1,0)、C(0,1),
 ∴OA1=OC=1,
∴OA1=OC=1,
∵∠A1OC=90°,
∴A1C=
=
,∠OA1C=∠OCA1=45°,
∵以A1C为一边向外作长宽比为
:1的矩形,
∴A1B1=
A1C=2,∠B1A1A2=180°-90°-45°=45°,
∴△A1A2B1是等腰直角三角形,
∴A1A2=
A1B1=2
.
如图,作三角形A1A2B1的高B1D,则A1D=B1D=
A1A2=
,
∴OD=OA1+A1D=1+
,
∴点B1的坐标为(1+
,
);
过点B2作B2E⊥x轴于点E,
易证三角形A2A3B2是等腰直角三角形,
∵A2B1=A1B1=2,
∴A2B2=
A2B1=2
,
∴A2A3=
A2B2=4,
∴B2E=
A2A3=2,
∴S△A1A2B2=
A1A2•B2E=
×2
×2=2
;
 (2)过点B3作B3F⊥x轴于点F,
(2)过点B3作B3F⊥x轴于点F,
易证三角形A3A4B3是等腰直角三角形,
∵A3B2=A2B2=2
,
∴A3B3=
A3B2=4,
∴A3A4=
A3B3=4
,
∴B3F=
A3A4=2
,
∴S△A2A3B3=
A2A3•B3F=
×4×2
=4
;
同理,可得S△A3A4B4=
×4
×4=8
;
…
S△AnAn+1Bn+1=2n
;
∴S△A1A2B2+S△A2A3B3+…+S△AnAn+1Bn+1=2
+4
+8
+…+2n
=
(2+4+8+…+2n)=
×
=(2n+1-2)
.
故答案为(1+
,
),2
;(2n+1-2)
.
 ∴OA1=OC=1,
∴OA1=OC=1,∵∠A1OC=90°,
∴A1C=
O
|
| 2 |
∵以A1C为一边向外作长宽比为
| 2 |
∴A1B1=
| 2 |
∴△A1A2B1是等腰直角三角形,
∴A1A2=
| 2 |
| 2 |
如图,作三角形A1A2B1的高B1D,则A1D=B1D=
| 1 |
| 2 |
| 2 |
∴OD=OA1+A1D=1+
| 2 |
∴点B1的坐标为(1+
| 2 |
| 2 |
过点B2作B2E⊥x轴于点E,
易证三角形A2A3B2是等腰直角三角形,
∵A2B1=A1B1=2,
∴A2B2=
| 2 |
| 2 |
∴A2A3=
| 2 |
∴B2E=
| 1 |
| 2 |
∴S△A1A2B2=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
 (2)过点B3作B3F⊥x轴于点F,
(2)过点B3作B3F⊥x轴于点F,易证三角形A3A4B3是等腰直角三角形,
∵A3B2=A2B2=2
| 2 |
∴A3B3=
| 2 |
∴A3A4=
| 2 |
| 2 |
∴B3F=
| 1 |
| 2 |
| 2 |
∴S△A2A3B3=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
同理,可得S△A3A4B4=
| 1 |
| 2 |
| 2 |
| 2 |
…
S△AnAn+1Bn+1=2n
| 2 |
∴S△A1A2B2+S△A2A3B3+…+S△AnAn+1Bn+1=2
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2(1-2n) |
| 1-2 |
| 2 |
故答案为(1+
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了矩形的性质,等腰直角三角形的判定与性质,相似三角形的判定与性质,三角形的面积,等比数列的求和,综合性较强,有一定难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知A1(0,1),
如图,已知A1(0,1),
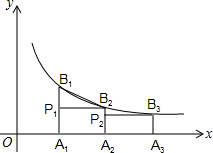 如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y=
如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y=