题目内容
已知抛物线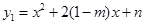 经过点(
经过点(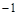 ,
,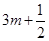 ).
).
(1)求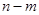 的值;
的值;
(2)若此抛物线的顶点为(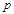 ,
,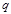 ),用含
),用含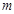 的式子分别表示
的式子分别表示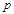 和
和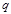 ,并求
,并求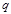 与
与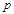 之间的函数关系式;
之间的函数关系式;
(3)若一次函数 ,且对于任意的实数
,且对于任意的实数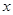 ,都有
,都有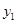 ≥
≥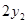 ,直接写出
,直接写出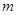 的取值范围.
的取值范围.
(1)n-m=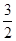 (2)q=-p2+p+
(2)q=-p2+p+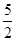 (3)-
(3)-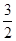 ≤m≤
≤m≤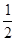 且m≠0
且m≠0
解析试题分析(1) ∵点(-1,3m+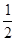 )经过抛物线,∴代入解析式得出n-m的值(2)将点(p,q)代入解析式。解:(1)∵抛物线
)经过抛物线,∴代入解析式得出n-m的值(2)将点(p,q)代入解析式。解:(1)∵抛物线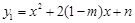 经过点(
经过点(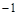 ,
,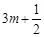 ),
),
∴ .
.
∴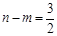 . ............................................................. 1分
. ............................................................. 1分
(2)∵ ,
,
∴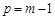 , ............................................................. 2分
, ............................................................. 2分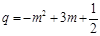 . .......................................................... 3分
. .......................................................... 3分
∵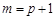 ,
,
∴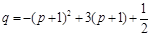 .
.
∴ . ........................................................ 5分
. ........................................................ 5分
(3) 的取值范围为
的取值范围为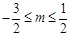 且
且 . .................................... 7分
. .................................... 7分
阅卷说明:只写 或只写
或只写 得1分.
得1分.
考点:二次函数的性质,不等式的解法。
点评:本题(1)问较简单,将坐标点代入即可求之。(2)问由(1)知m n 的关系,将点(p,q)代入就能得到解析式 (3)构建不等式,由y1 y2的解析式得到,注意解不等式时的性质。本题属于中难题。计算量较大,易出错。

练习册系列答案
相关题目
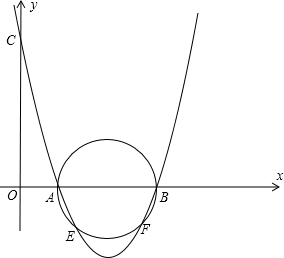 已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆.
已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆. 如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.
如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.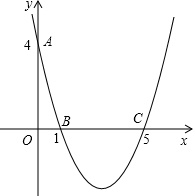 如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.