题目内容
 如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.
如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.(1)求证:四边形EFGH是矩形;
(2)若E、F、G、H分别是OA、OB、OC、OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.
分析:(1)首先证明四边形EFGH是平行四边形,然后再证明HF=EG;
(2)根据题干求出矩形的边长CD和BC,然后根据矩形面积公式求得.
(2)根据题干求出矩形的边长CD和BC,然后根据矩形面积公式求得.
解答:(1) 证明:∵四边形ABCD是矩形,
证明:∵四边形ABCD是矩形,
∴OA=0B=OC=OD,
∵AE=BF=CG=DH,
∴AO-AE=OB-BF=CO-CG=DO-DH,
即:OE=OF=OG=OH,
∴四边形EFGH是矩形;
(2)解:∵G是OC的中点,
∴GO=GC,
∵DG⊥AC,
∴∠DGO=∠DGC=90°,
又∵DG=DG,
∴△DGC≌△DGO,
∴CD=OD,
∵F是BO中点,OF=2cm,
∴BO=4cm,
∵四边形ABCD是矩形,
∴DO=BO=4cm,
∴DC=4cm,DB=8cm,
∴CB=
=4
,
∴矩形ABCD的面积=4×4
=16
cm2.
 证明:∵四边形ABCD是矩形,
证明:∵四边形ABCD是矩形,∴OA=0B=OC=OD,
∵AE=BF=CG=DH,
∴AO-AE=OB-BF=CO-CG=DO-DH,
即:OE=OF=OG=OH,
∴四边形EFGH是矩形;
(2)解:∵G是OC的中点,
∴GO=GC,
∵DG⊥AC,
∴∠DGO=∠DGC=90°,
又∵DG=DG,
∴△DGC≌△DGO,
∴CD=OD,
∵F是BO中点,OF=2cm,
∴BO=4cm,
∵四边形ABCD是矩形,
∴DO=BO=4cm,
∴DC=4cm,DB=8cm,
∴CB=
| DB2-DC2 |
| 3 |
∴矩形ABCD的面积=4×4
| 3 |
| 3 |
点评:本题主要考查矩形的判定,首先要判定四边形是平行四边形,然后证明对角线相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

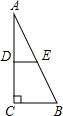 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )