Question

【题目】如图，等腰三角形的一边在轴的正半轴上，点的坐标为， ，动点从原点出发，在线段上以每秒2个单位的速度向点匀速运动，动点从原点出发，沿轴的正半轴以每秒1个单位的速度向上匀速运动，过点作轴的平行线分别交于，设动点，同时出发，当点到达点时，点也停止运动，他们运动的时间为秒 ．

（1）点的坐标为_____,的坐标为____；

（2）当为何值时，四边形为平行四边形；

（3）是否存在某一时刻，使为直角三角形？若存在，请求出此时的值；若不存在，请说明理由．

Answer 1

【答案】（1）（t，t），（10-t，t）；（2）当t为时，四边形POEF是平行四边形；（3）t=和4时，使△PEF为直角三角形．

【解析】

（1）过点A作AD⊥OB，由点A的坐标为（6，8），可得OD=6，AD=8，然后由勾股定理得：OA=10，由OA=OB可得：OB=10，进而可得：BD=4，进而可得点B的坐标为：（10，0），然后设OA的关系式：y=kx，然后将A（6，8）代入即可得直线OA的关系式，然后设直线AB的关系式为：y=kx+b，然后将A，B两点代入，即可确定直线AB的关系式，由过点Q作x轴的平行线分别交OA，AB于E，F，可知点Q、E、F三点的纵坐标相等均为t，然后由点E在OA上，点F在AB上，将点E、F的纵坐标分别代入对应的关系式，即可得到得到点E、F的坐标；
（2）由EF∥OP，欲使四边形POEF是平行四边形，只需EF=OP即可，从而可得关于t的等式，解答即可；
（3）分三种情况讨论：①PE⊥EF，②PE⊥PF，③EF⊥PF即可．

解：（1）过点A作AD⊥OB，垂足为D，如图1，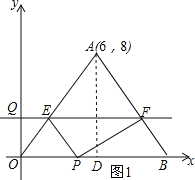

∵点A的坐标为（6，8），
∴OD=6，AD=8，
由勾股定理得：OA=10，
∵OA=OB，
∴OB=10，
∴BD=4，
∴点B的坐标为：（10，0），
设直线OA的关系式：y=kx，
将A（6，8）代入上式，得：
6k=8，
解得：k=，
所以直线OA的关系式：y=x，
设直线AB的关系式为：y=kx+b，
将A，B两点代入上式得：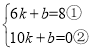
，
解得： ，
所以直线AB的关系式为：y=-2x+20，
∵过点Q作x轴的平行线分别交OA，AB于E，F，
∴点Q、E、F三点的纵坐标相等，
∵动点Q从原点O出发，沿y轴的正半轴以每秒1个单位的速度向上匀速运动，
动点P从原点O出发，在线段OB上以每秒2个单位的速度向点B匀速运动，
∴t秒后，OQ=t，OP=2t，
∴Q、E、F三点的纵坐标均为t，
将点E的纵坐标t代入y=x，得：x=t，
∴E点的坐标为：（t，t），
将点E的纵坐标t代入y=-2x+20，得：x=10-t，
∴F点的坐标为：（10-t，t），
故答案为：（t，t），（10-t，t）；
（2）由（1）知：E（t，t），F（10-t，t），
∴EF=10-t-t=10-t，
∵四边形POEF是平行四边形，
∴EF∥OP，且EF=OP，
即10-t=2t，
解得：t=，
∴当t为时，四边形POEF是平行四边形；
（3）过点E作EM⊥OB，垂足为M，过点F作FN⊥OB，垂足为N，
可得四边形EMNF是矩形，如图2，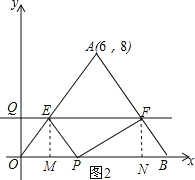

①当PE⊥PF时，PE2+PF2=EF2，
由（1）知：OM=t，EM=FN=t，ON=10-t，EF=10-t，
∴PM=t，PN=10-t，
∵PE2=ME2+MP2，PF2=PN2+FN2，
∴t2+（t）2+（10-t）2+t2=（10-t）2，
解得：t1=0（舍去），t2=；
②当PE⊥EF时，如图3，可得四边形EPNF是矩形，

∵四边形EPNF是矩形，
∴EF=PN，
即：EF=ON-OP，
∴10-t=10-t-2t，
解得t=0（舍去）；
③当EF⊥PF时，如图4，可得四边形EMPF是矩形，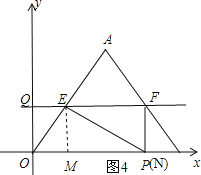

∵四边形EMPF是矩形，
∴EF=MP，
即EF=OP-OM，
∴10-t=2t-t，
解得：t=4，
∴当t=和4时，使△PEF为直角三角形．