题目内容
16.已知a△b=ab+(a-b),例如:2△3=2×3+(2-3)=5,求:sin30°△(tan45°-tan60°)的值.分析 根据题目所给的运算法则求解.
解答 解:原式=$\frac{1}{2}$△(1-$\sqrt{3}$)
=$\frac{1}{2}$×(1-$\sqrt{3}$)+($\frac{1}{2}$-1+$\sqrt{3}$)
=$\frac{\sqrt{3}}{2}$.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
相关题目
1.直线y=$\frac{1}{2}$x+b与直线y=-2x+2的交点不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.把抛物线y=-$\frac{1}{2}$x2向下平移1个单位,再向左平移1个单位,得到的抛物线解析式为( )
| A. | y=-$\frac{1}{2}$(x+1)2+1 | B. | y=-$\frac{1}{2}$(x+1)2-1 | C. | y=-$\frac{1}{2}$(x-1)2+1 | D. | y=-$\frac{1}{2}$(x-1)2-1 |
 直线l经过第二,三,四象限,l的解析式是y=(m+1)x-n,则m的取值范围在数轴上表示为( )
直线l经过第二,三,四象限,l的解析式是y=(m+1)x-n,则m的取值范围在数轴上表示为( )




 如图,正方形ABCD的对角线BD长为2$\sqrt{2}$,若直线满足:(1)点D到直线的距离为1;(2)A、C两点到直线的距离相等,则符合题意的直线的条数为( )
如图,正方形ABCD的对角线BD长为2$\sqrt{2}$,若直线满足:(1)点D到直线的距离为1;(2)A、C两点到直线的距离相等,则符合题意的直线的条数为( )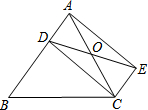 如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.
如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.