题目内容
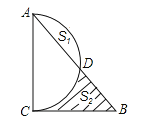
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 上一点,且点
上一点,且点![]() 不与点
不与点![]() 重合,点
重合,点![]() 为半径
为半径![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:点![]() 为
为![]() 的中点;
的中点;
(2)连接![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
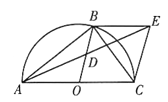
【答案】(1)证明见解析;(2)6.
【解析】
(1)证明△ADO≌△EDB,可得AD=CD,即可说明D为AE的中点;
(2)过点B作BF⊥AC垂足为F,过点D作DG⊥AC垂足于G,由(1)知![]() ,根据面积公式可求BF长,再通过证明
,根据面积公式可求BF长,再通过证明![]() ,利用相似比求出DG长,进而求得三角形ADO的面积.
,利用相似比求出DG长,进而求得三角形ADO的面积.
(1)证明:
∵D为BO的中点,
∴OD=BD
又∵BE∥AC,
∴∠EBO=∠AOD,
在△ADO和△EDB中,
 ,
,
∴△ADO≌△EDB,
∴AD=ED,
∴点D是AE的中点.
(2)过点B作BF⊥AC垂足为F,过点D作DG⊥AC垂足于G,

由(1)知△ADO≌△EDB,
∴![]() ,
,
∵AC为圆的直径,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵点D为BO的中点,
∴![]() ,
,
∵DG⊥AC,BF⊥AC,
∴DG∥BF,
∴△DOG∽△BOF,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为:6.

练习册系列答案
相关题目