题目内容
8．化简求值，$\frac{m}{m+3}$-$\frac{6}{{m}^{2}-9}$+$\frac{2}{m-3}$，其中m=-5．分析 先通分，然后将同分母相加减，最后把m=-5代入化简后的式子，就可解决问题．
解答 解：当m=-5时，原式=$\frac{m（m-3）}{（m+3）（m-3）}$-$\frac{6}{{m}^{2}-9}$+$\frac{2（m+3）}{（m+3）（m-3）}$
=$\frac{{m}^{2}-3m}{{m}^{2}-9}$-$\frac{6}{{m}^{2}-9}$+$\frac{2m+6}{{m}^{2}-9}$=$\frac{{m}^{2}-3m-6+2m+6}{{m}^{2}-9}$
=$\frac{{m}^{2}-m}{{m}^{2}-9}$=$\frac{25-（-5）}{25-9}$=$\frac{30}{16}$=$\frac{15}{8}$．
点评 本题主要考查分式的化简求值，通过通分将异分母化为同分母，是解决本题的关键．
练习册系列答案
相关题目
16．对车间10名工人上月生产情况进行统计，结果如下所示（单位：件），则这10名工人上个月平均每人生产14.4件．
| 产量（件） | 40 | 30 | 10 | 8 |
| 人数（人） | 1 | 1 | 5 | 3 |
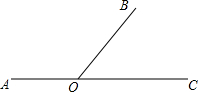如图，A、O、C在同一直线上，
