题目内容
【题目】为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.
(1)求y与x的函数表达式;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
【答案】(1)![]() (
(![]() 为整数,且
为整数,且![]() );(2)费用最省的方案为购买A种树苗11棵,B种树苗10棵,此时所需费用为1690元
);(2)费用最省的方案为购买A种树苗11棵,B种树苗10棵,此时所需费用为1690元
【解析】
(1)根据题意可知购买A种树苗![]() 棵,然后根据总费用=A种树苗的总费用+B种树苗的总费用进一步列出式子加以化简即可;
棵,然后根据总费用=A种树苗的总费用+B种树苗的总费用进一步列出式子加以化简即可;
(2)根据购买B种树苗的数量少于A种树苗的数量可得关于![]() 的一元一次不等式,解出不等式得到
的一元一次不等式,解出不等式得到![]() 的范围,然后进一步分析求解即可.
的范围,然后进一步分析求解即可.
(1)设购买B种树苗![]() 棵,则购买A种树苗
棵,则购买A种树苗![]() 棵,
棵,
由已知得:![]() (
(![]() 为整数,且
为整数,且![]() );
);
(2)∵购买B种树苗的数量少于A种树苗的数量,
∴![]() ,
,
解得:![]()
∵![]() 中
中![]() ,
,
∴当![]() 时,
时,![]() 取最小值,最小值为1690.
取最小值,最小值为1690.
答:费用最省的方案为购买A种树苗11棵,B种树苗10棵,此时所需费用为1690元.

 应用题作业本系列答案
应用题作业本系列答案【题目】临近期末,历史老师为了了解所任教的甲、乙两班学生的历史基础知识背诵情况,从甲、乙两个班学生中分别随机抽取了20名学生来进行历史基础知识背诵检测,满分50分,得到学生的分数相关数据如下:
甲 | 32 | 35 | 46 | 23 | 41 | 49 | 37 | 41 | 36 | 41 |
37 | 44 | 39 | 46 | 46 | 41 | 50 | 43 | 44 | 49 |
乙 | 25 | 34 | 43 | 46 | 35 | 41 | 42 | 46 | 44 | 42 |
47 | 45 | 42 | 34 | 39 | 47 | 49 | 48 | 45 | 42 |
通过整理,分析数据:两组数据的平均数、中位数、众数如下表:
平均数(分) | 中位数(分) | 众数(分) | |
甲 | 41 | 41 |
|
乙 | 41.8 |
| 42 |
历史老师将乙班成绩按分数段(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示分数)绘制成扇形统计图,如图(不完整)
表示分数)绘制成扇形统计图,如图(不完整)
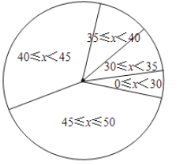
请回答下列问题:
(1)![]() _______分;
_______分;
(2)扇形统计图中,![]() 所对应的圆心角为________度;
所对应的圆心角为________度;
(3)请结合以上数据说明哪个班背诵情况更好(列举两条理由即可).