题目内容
【题目】(1)操作发现
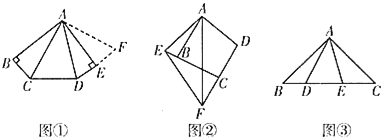
如图①,在五边形![]() 中,
中,![]() ,
,![]() ,试猜想
,试猜想![]() 之间的数量关系,小明经过仔细思考,得到如下解题思路:将
之间的数量关系,小明经过仔细思考,得到如下解题思路:将![]() 绕点
绕点![]() 逆时针旋转90°至
逆时针旋转90°至![]() ,由
,由![]() ,得
,得![]() ,即点
,即点![]() 三点共线,易证
三点共线,易证![]() ,故
,故![]() 之间的数量关系是________;
之间的数量关系是________;
(2)类比探究
如图②,在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() 的延长线上,
的延长线上,![]() ,连接
,连接![]() ,试猜想
,试猜想![]() 之间的数量关系,并给出证明;
之间的数量关系,并给出证明;
(3)拓展延伸
如图③,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 均在边
均在边![]() 上,且
上,且![]() ,若
,若![]() ,则
,则![]() 的长为________.
的长为________.
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() .
.
【解析】
(1)如图1,将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌△AFD,可得结论;
(2)如图2,将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',证明△AFE≌△AFE',据全等三角形的性质解答;
(3)将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',根据全等三角形的性质、勾股定理计算.
(1)BC,CD,DE之间的数量关系为:![]() ,理由是:
,理由是:
如图1,将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=∠AEF=90°,得∠DEF=180°,即点D,E,F三点共线,

∵∠BAE=90°,∠CAD=45°,
∴∠BAC+∠DAE=∠DAE+∠EAF=45°,
∴∠CAD=∠FAD,
∵AD=AD,
∴△ACD≌△AFD(SAS),
∴CD=DF=DE+EF=DE+BC,
故答案为: CD=DE+BC;
(2)如图2,![]() 之间的数量关系是
之间的数量关系是![]() ,
,
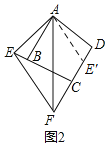
证明:将![]() 绕点
绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 与
与![]() 重合,得到
重合,得到![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
![]() ,即
,即![]() 三点共线,
三点共线,
又![]() ,
,
∴![]() ,在
,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
(3)如图3,将![]() 绕点
绕点![]() 逆时针旋转至
逆时针旋转至![]() ,使
,使![]() 与
与![]() 重合,连接
重合,连接![]() ,则
,则![]() ,
,
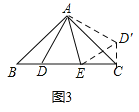
由(1)同理得,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() .
.

 期末集结号系列答案
期末集结号系列答案【题目】七(2)班共有50名学生,老师安排每人制作一件![]() 型或
型或![]() 型的陶艺品,学校现有甲种制作材料36
型的陶艺品,学校现有甲种制作材料36![]() ,乙种制作材料29
,乙种制作材料29![]() ,制作
,制作![]() 、
、![]() 两种型号的陶艺品用料情况如下表:
两种型号的陶艺品用料情况如下表:
需甲种材料 | 需乙种材料 | |
1件 | 0.9 | 0.3 |
1件 | 0.4 | 1 |
(1)设制作![]() 型陶艺品
型陶艺品![]() 件,求
件,求![]() 的取值范围;
的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作![]() 型和
型和![]() 型陶艺品的件数.
型陶艺品的件数.
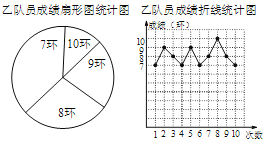
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员举行了一次选拔赛,要求这两名队员各射击10次.比赛结束后,根据比赛成绩情况,将甲、乙两名队员的比赛成绩制成了如下的统计图(表):
甲队员的成绩统计表
成绩(单位:环) | 7 | 8 | 9 | 10 |
次数(单位:次) | 5 | 1 | 2 | 2 |
(1)在图1中,求“8环”所在扇形的圆心角的度数;
(2)经过整理,得到的分析数据如表,求表中的a、b、c的值.
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 | c |
乙 | a | b | 7 | 1 |
(3)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.
【题目】甲、乙人5场10次投篮命中次数如图
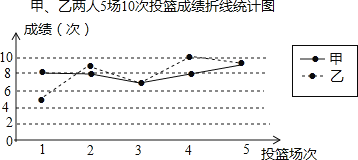
(1)填写表格.
平均数 | 众数 | 中位数 | 方差 | |
甲 | ______ | 8 | 8 | ______ |
乙 | 8 | ______ | ______ | 3.2 |
(2)①教练根据这5个成绩,选择甲参加投篮比赛,理由是什么?
②如果乙再投篮1场,命中8次,那么乙的投监成绩的方差将会怎样变化?(“变大”“变小”或”不变”)