题目内容
【题目】如图,OD 是∠AOB 的平分线,∠AOC=2∠BOC.
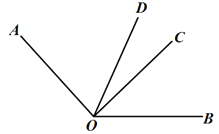
(1)若 AO⊥CO,求∠BOD 的度数;
(2)若∠COD=21°,求∠AOB 的度数.
【答案】(1)67.5![]() , (2)126
, (2)126![]() .
.
【解析】
(1)由垂直可得∠AOC=90°,由∠AOC=2∠BOC得∠BOC的度数,即可得∠AOB的度数,然后根据角平分线的定义可知∠AOD=∠BOD=![]() ,计算即可求出;
,计算即可求出;
(2)由∠AOC=2∠BOC得∠AOB=3∠BOC ,然后根据角平分线的定义可知∠AOD=∠BOD=![]() ,再由∠COD=∠BOD-∠BOC =21°可先求得∠BOC,即可得∠AOB 的度数.
,再由∠COD=∠BOD-∠BOC =21°可先求得∠BOC,即可得∠AOB 的度数.
(1)∵AO![]()
∵∠AOC=90°
∵∠AOC=2∠BOC
∴∠BOC=45°
∴∠AOB=∠AOC+∠BOC=135![]()
∵OD平分∠AOB
∴∠BOD=![]() =67.5
=67.5![]() ;
;
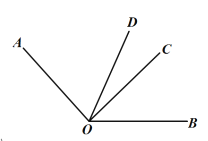
(2)∵∠AOC=2∠BOC
∴∠AOB=∠AOC+∠BOC =3∠BOC
∵OD平分∠AOB
∴∠BOD=![]() ∠AOB=
∠AOB=![]() ∠BOC
∠BOC
∴∠COD=∠BOD-∠BOC=![]() ∠BOC
∠BOC
∵∠COD=21![]()
∴∠BOC=42°
∴∠AOB =3∠BOC = 126![]() .
.
故答案为:(1)67.5![]() , (2)126
, (2)126![]() .
.

练习册系列答案
相关题目