Question

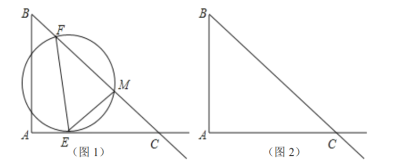
【题目】如图，RT△ABC中，，. 动点同时分别从点出发，分别沿着射线和射线的方向均以每秒1个单位的速度运动，连接，以为直径作交射线于点，连接，设运动的时间为.

（1）当点在线段上时，用关于的代数式表示________，________. （直接写出结果）

（2）在整个运动过程中，当为何值时，以点、、为顶点的三角形与以点、、为顶点的三角形相似？

Answer 1

【答案】（1），；（2）见解析.

【解析】

（1）当点E在线段AC上时，由题意可知AE=t,则CE=AC-AE=8-t,；利用圆周角定理可证得∠EMF=90°，可证△CEM∽△CBA,利用对应边成比例可表示出CM；

（2）分三种情况讨论，即0<t≤8, 8<t≤10,t≥10.每种情况均用△CEM∽△CBA表示EM和CM长，从而表示FM长，再由△FEM∽△BCA或△EFM∽△BCA，得出 或，即可求出t值.

解：（1），；

理由：∵AE=t,AC=8，

∴CE=8-t，

∵EF是圆的直径，

∴∠EMF=90°，

∴∠EMC=∠BAC=90°，

∵∠MCE=∠ACB，

∴△MCE∽△ACB，

∴ ，

在Rt△ABC中，AC=8，AB=6, ∴BC=10，

∴，

∴CM= ；

（2）当时，如图，由题意得，

，

若，此时，则，即（舍去），

若，此时，则，即；

解得（成立）；

当时，如图，由题意得：，

，

此时，所以不成立；

若，，则，即；

解得（成立）；

当时，如图，由题意得：，

，

若，此时，则，即；

解得（成立）；

若，此时，则，即；

解得（舍去）；

综上所述，当，或时，以点、、为顶点的三角形与相似.