题目内容
4. 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向C点以2cm/s的速度移动.
如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向C点以2cm/s的速度移动.(1)如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于8cm2?
(2)在(1)中,△PBQ的面积能否等于△ABC面积的一半?说明理由;
(3)几秒后,点P,点Q相距4$\sqrt{2}$cm?
分析 (1)设经过x秒钟,使△PBQ的面积为8cm2,得到BP=6-x,BQ=2x,根据三角形的面积公式得出方程$\frac{1}{2}$×(6-x)×2x=8,求出即可;
(2)△ABC面积为36cm2,同(1)列方程解答即可;
(3)设t秒后,点P,点Q相距4$\sqrt{2}$cm,依题意得BP=6-t,BQ=2t,利用勾股定理列方程求解.
解答 解:(1)设经过x秒钟,使△PBQ的面积为8cm2,
BP=6-x,BQ=2x,
∵∠B=90°,
∴$\frac{1}{2}$BP×BQ=8,
∴$\frac{1}{2}$(6-x)×2x=8,
∴x1=2,x2=4.
答:如果点P、Q分别从A、B同时出发,经过2或4秒钟,使△PBQ的面积为8cm2.
(2)由题意得$\frac{1}{2}$BP×BQ=$\frac{1}{2}$×$\frac{1}{2}$×12×6,
$\frac{1}{2}$(6-x)×2x=18,
x2-6x+18=0,
△=36-72=-36<0,
此方程无解,△PBQ的面积不能等于△ABC面积的一半;
(3)设t秒后,点P,点Q相距4$\sqrt{2}$cm,由题意得:
(2t)2+(6-t)2=32,
整理得:(5x-2)(x-2)=0,
解得:x1=$\frac{2}{5}$,x2=2,
∵BC=3cm,
∴x=2不合题意.
答:$\frac{2}{5}$秒后,点P,点Q相距4$\sqrt{2}$cm.
点评 此题主要考查了一元二次方程的应用,关键是利用三角形的面积与勾股定理得出等量关系解决问题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
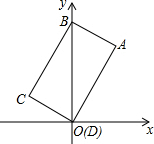 如图,把矩形ABCD按如图所示方式放置,若点A的坐标为(2,3),点B的坐标为(0,4).
如图,把矩形ABCD按如图所示方式放置,若点A的坐标为(2,3),点B的坐标为(0,4).