题目内容
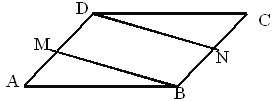
【题目】已知：在平行四边形ABCD中，AM=CN.求证：四边形MBND是平行四边形.
【答案】证明见解析.
【解析】可通过证明DM∥BN，DM=BN来说明四边形是平行四边形，也可通过DM=BN，BM=DN来说明四边形是平行四边形．
（法一）∵四边形ABCD是平行四边形，
∴AD∥CB，AD=CB．
∵AM=CN，
∴AD﹣AM=CB﹣CN，
即DM=BN．
又∵DM∥BN，
∴四边形MBND是平行四边形．
（法二）∵四边形ABCD是平行四边形，
∴∠A=∠C，AB=CD，
在△AMN和△CND中，
又∵
，
∴△AMN≌△CND，
∴BM=DN．
∵AM=CN，
∴AD﹣AM=CB﹣CN，
即DM=BN．
又∵BM=DN，
∴四边形MBND是平行四边形．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
【题目】阅读下列解题过程：
=
=
=
-2；
=
=
．
请回答下列问题：
（1）观察上面的解题过程，请直接写出式子
= ；
（2）观察上面的解题过程，请直接写出式子
= ；
（3）利用上面所提供的解法，请求
+···+
的值．
【题目】甲、乙两名队员参加射击训练(各射击10次)，成绩分别被制成下列两个统计图：
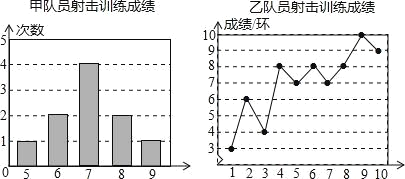
根据以上信息，整理分析数据如下表：
平均成绩（环） | 中位数（环） | 众数（环） | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | c | d |
（1）填空：a＝ ，b＝ ，c＝ ，求出 d 的值；
（2）若选派其中一名参赛，你认为应选哪名队员?请说明理由．
