题目内容
 如图,△CED、△BFE都是由△ABC经过平移得到的像.D、E、F三点在同一直线上.
如图,△CED、△BFE都是由△ABC经过平移得到的像.D、E、F三点在同一直线上.(1)试说明DF=2CB成立的理由;
(2)△ECB≌△ABC吗?请说明你的理由.
分析:(1)根据平移的性质可求出BC=EF=DE,且D、E、F三点在同一直线上,即DF=2CB;
(2)根据平移的性质,AC=EB,EC=AB,BC为公共边,利用判定三角形全等的判定性质,即可得出△ECB≌△ABC.
(2)根据平移的性质,AC=EB,EC=AB,BC为公共边,利用判定三角形全等的判定性质,即可得出△ECB≌△ABC.
解答:解:(1)因为△CED、△BFE都是由△ABC经过平移得到的像
所以DE=BC,EF=BC.(2分)
所以DF=DE+EF=2BC.(2分)
(2)△ECB≌△ABC(1分)
理由如下:∵△CED、△BFE都是由△ABC经过平移得到的像
∴AC=EB,EC=AB(2分)
在△ECB≌△ABC中
∴△ECB≌△ABC(SSS)(2分)
所以DE=BC,EF=BC.(2分)
所以DF=DE+EF=2BC.(2分)
(2)△ECB≌△ABC(1分)
理由如下:∵△CED、△BFE都是由△ABC经过平移得到的像
∴AC=EB,EC=AB(2分)
在△ECB≌△ABC中
|
∴△ECB≌△ABC(SSS)(2分)
点评:解答此题的关键是要熟知平移的性质:经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等;平移变换不改变图形的形状、大小和方向.

练习册系列答案
相关题目
 如图是由一副直角三角尺拼成的图形,请写出一对相似的三角形:
如图是由一副直角三角尺拼成的图形,请写出一对相似的三角形: 如图,下列推理正确的是( )
如图,下列推理正确的是( ) 如图,已知点E为矩形ABCD的边BC的中点,BF⊥CE于F,
如图,已知点E为矩形ABCD的边BC的中点,BF⊥CE于F,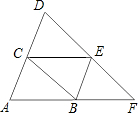 如图,△CED、△BFE都是由△ABC经过平移得到的像.D、E、F三点在同一直线上.
如图,△CED、△BFE都是由△ABC经过平移得到的像.D、E、F三点在同一直线上.