题目内容
12．阅读材料：求1+2+22+23+24+…+22013的值．解：设S=1+2+22+23+24+…+22012+22013，将等式两边同时乘以2得：
2S=2+22+23+24+25+…+22013+22014
将下式减去上式得2S-S=22014-1
即S=22014-1
即1+2+22+23+24+…+22013=22014-1
仿照此法计算：1+2+22+23+…+2100．
分析 设S=1+2+22+23+24+…+2100，两边乘以2后得到关系式，与已知等式相减，变形即可求出所求式子的值．
解答 解：（1）设S=1+2+22+23+24+…+2100，
将等式两边同时乘以2得：2S=2+22+23+24+…+210+2101，
将下式减去上式得：2S-S=2101-1，即S=2101-1，
则1+2+22+23+24+…+2100=2101-1．
点评 此题考查了同底数幂的乘法，弄清题中的技巧是解本题的关键．
练习册系列答案
相关题目
20．夜晚当你靠近一盏路灯时，你发现自己的影子是（ ）
| A． | 变短 | B． | 变长 | C． | 由短变长 | D． | 由长变短 |
7．
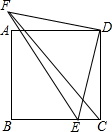如图，在正方形ABCD中，E是BC上的动点（不与点B、C重合），连接DE，过点D作FD⊥ED于点D，并使FD=ED，连接CF，EF，下列角的大小比较中，一定正确的是（ ）
如图，在正方形ABCD中，E是BC上的动点（不与点B、C重合），连接DE，过点D作FD⊥ED于点D，并使FD=ED，连接CF，EF，下列角的大小比较中，一定正确的是（ ）| A． | ∠ADF＞∠CDE | B． | ∠DCF＞∠DFC | C． | ∠DFC＞∠ADF | D． | ∠DEC＞∠BEF |
小明同学骑自行车去郊外春游，如图表示他离家的距离y（千米）与所用的时间x（小时）之间关系的函数图象．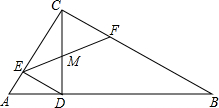
已知△ABC中，∠ACB=90°，AC=3，tanA=$\frac{4}{3}$，CD⊥AB于点D，DE⊥AC，点F在线段BC上，EF交CD于点M．