题目内容
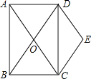
【题目】如图，矩形
的对角线
，
相交于点
，
关于
的对称图形为
．
（1）求证：四边形
是菱形；
（2）连接
，交于点
，连接
，取的中点
，连接
．
①根据题意补全图形；
②若
＝
，请用等式表示线段
、
、之间的数量关系，并证明你的结论．
【答案】（1）见解析；（2）①见解析，②
＝
，见解析
【解析】
（1）根据四边相等的四边形是菱形即可判断．
（2）①根据要求图形即可．
②线段
、
、
之间的数量关系是：
．取的中点
，连接
，
，
，首先证明四边形
是菱形，推出
是
的中位线，再根据勾股定理即可解决问题．
解：
（1）证明：∵ 四边形
是矩形，
∴ 
与
相等且互相平分，
∴ 
＝
，
∵ 
关于
的对称图形为
，
∴ ＝
，
＝
，
∴ ＝＝＝，
∴ 四边形
是菱形．
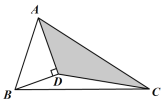
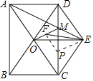
（2）①如图．
②线段
、
、
之间的数量关系是：
＝
．
证明：取的中点
，连接
，
，
，
∵ 四边形是矩形∴ 
＝
∵ 
＝
，
∴ 
＝
＝
∵ 
＝，
∴ 
是等边三角形，
∴ 
＝，
∵ 四边形是菱形，
∴ ＝，
＝
＝，
，
∴ 四边形
是菱形，
∴ 
，
∴ 
，即
＝，
∵ 
是
的中位线，
∴ 
，
，
∴ ＝
＝，
∵ 是的中点，
∴ ＝
，
∴ 
＝
＝，
∴ 
＝，
∴ 
＝
＝，
根据勾股定理得：
＝
，
即：
＝，
∴ ＝．
练习册系列答案
相关题目
