题目内容
已知点(﹣1,y1),(2,y2),(3,y3)在反比例函数y=
 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y1>y2 D.y2>y3>y1
B【考点】反比例函数图象上点的坐标特征.
【专题】压轴题.
【分析】先判断出函数反比例函数y=
 的图象所在的象限,再根据图象在每一象限的增减性及每一象限坐标的特点进行判断即可.
的图象所在的象限,再根据图象在每一象限的增减性及每一象限坐标的特点进行判断即可.
【解答】解:∵k2≥0,∴﹣k2≤0,﹣k2﹣1<0,
∴反比例函数y=
 的图象在二、四象限,
的图象在二、四象限,
∵点(﹣1,y1)的横坐标为﹣1<0,∴此点在第二象限,y1>0;
∵(2,y2),(3,y3)的横坐标3>2>0,∴两点均在第四象限y2<0,y3<0,
∵在第四象限内y随x的增大而增大,
∴0>y3>y2,
∴y1>y3>y2.
故选:B.
【点评】本题考查了反比例函数图象上点的坐标特征:当k>0时,图象分别位于第一、三象限,横纵坐标同号;当k<0时,图象分别位于第二、四象限,横纵坐标异号.

练习册系列答案
相关题目
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
|
| 甲 | 乙 |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.

 C.5 D.
C.5 D.

 中第一个方程y的系数和第二个方程x的系数看不到了,现在已知小丽的结果是
中第一个方程y的系数和第二个方程x的系数看不到了,现在已知小丽的结果是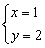 ,你能由此求出原来的方程组吗?
,你能由此求出原来的方程组吗?


 3y=7,则6
3y=7,则6