题目内容
某商店需要购进甲、乙两种商品共160件，其进价和售价如下表：
|
| 甲 | 乙 |
| 进价（元/件） | 15 | 35 |
| 售价（元/件） | 20 | 45 |
（1）若商店计划销售完这批商品后能获利1100元，问甲、乙两种商品应分别购进多少件？
（2）若商店计划投入资金少于4300元，且销售完这批商品后获利多于1260元，请问有哪几种购货方案？并直接写出其中获利最大的购货方案．
【考点】一元一次不等式组的应用；二元一次方程组的应用．
【专题】方案型；图表型．
【分析】（1）等量关系为：甲件数+乙件数=160；甲总利润+乙总利润=1100．
（2）设出所需未知数，甲进价×甲数量+乙进价×乙数量＜4300；甲总利润+乙总利润＞1260．
【解答】解：（1）设甲种商品应购进x件，乙种商品应购进y件．
根据题意得：
．
解得：
．
答：甲种商品购进100件，乙种商品购进60件．
（2）设甲种商品购进a件，则乙种商品购进（160﹣a）件．
根据题意得
．
解不等式组，得65＜a＜68．
∵a为非负整数，∴a取66，67．
∴160﹣a相应取94，93．
方案一：甲种商品购进66件，乙种商品购进94件．
方案二：甲种商品购进67件，乙种商品购进93件．
答：有两种购货方案，其中获利最大的是方案一．
【点评】解决本题的关键是读懂题意，找到所求量的等量关系及符合题意的不等关系式组：甲件数+乙件数=160；甲总利润+乙总利润=1100．甲进价×甲数量+乙进价×乙数量＜4300；甲总利润+乙总利润＞1260．
练习册系列答案
阅读快车系列答案
相关题目
商店某天销售了11件衬衫，其领口尺寸统计如下表：
| 领口尺寸(单位：cm) | 38 | 39 | 40 | 41 | 42 |
| 件数 | 1 | 4 | 3 | 1 | 2 |
则这ll件衬衫领口尺寸的众数是________cm，中位数是________cm．
（2）
（3）
A、1个 B、2个 C、3个 D、4个
，BC=2，求⊙O的半径．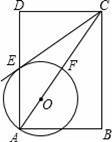
xa+1y-2b与-
x2-by2的是同类项，则ba的值为 .
枚，2分硬币有
枚，则可列方程组为 ．
的图象上．下列结论中正确的是（ ）