题目内容
已知x2+x-6是多项式2x4+x3-ax2+bx+a+b-1的因式,则a=________.
16
分析:设2x4+x3-ax2+bx+a+b-1=(x2+x-6)•A,当多项式等于0时,得到两个x的根,代入式子2x4+x3-ax2+bx+a+b-1,可求出a的值.
解答:令2x4+x3-ax2+bx+a+b-1=(x2+x-6)•A=(x+3)(x-2)•A.
取x=-3,x=2分别代入上式,
当x=-3时,2x4+x3-ax2+bx+a+b-1,
=2×81-27-9a-3b+a+b-1,
=134-8a-2b,
=0.
当x=2时,2x4+x3-ax2+bx+a+b-1,
=2×16+8-4a+2b+a+b-1,
=39-3a+3b,
=0.
根据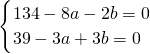 ,
,
可得a=16,b=3.
点评:本题考查了因式分解的应用和等式的应用,根据x的根,从而得出a,b的值.
分析:设2x4+x3-ax2+bx+a+b-1=(x2+x-6)•A,当多项式等于0时,得到两个x的根,代入式子2x4+x3-ax2+bx+a+b-1,可求出a的值.
解答:令2x4+x3-ax2+bx+a+b-1=(x2+x-6)•A=(x+3)(x-2)•A.
取x=-3,x=2分别代入上式,
当x=-3时,2x4+x3-ax2+bx+a+b-1,
=2×81-27-9a-3b+a+b-1,
=134-8a-2b,
=0.
当x=2时,2x4+x3-ax2+bx+a+b-1,
=2×16+8-4a+2b+a+b-1,
=39-3a+3b,
=0.
根据
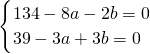 ,
,可得a=16,b=3.
点评:本题考查了因式分解的应用和等式的应用,根据x的根,从而得出a,b的值.

练习册系列答案
相关题目