题目内容
(1)计算:如图①,直径为a的三等圆⊙O1、⊙O2、⊙O3两两外切,切点分别为A、B、C ,求O1A的长(用含的代数式表示)。
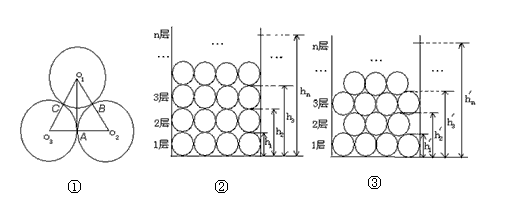
(2)探索:若干个直径为a的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放,探索并求出这两种方案中n层圆圈的高度hn和hn′(用含n、a的代数式表示);
(3)应用:现有长方体集装箱,其内空长为5米,宽为3.1米,高为3.1米,用这样的集装箱装运长为5米,底面直径(横截面的外圆直径)为0.1米的圆柱形钢管,你认为采用(2)中的哪种方案在该集装箱中装运钢管数最多?并求出一个这样的集装箱最多能装运多少根钢管?( ≈1.73)
≈1.73)
(3)应用:现有长方体集装箱,其内空长为5米,宽为3.1米,高为3.1米,用这样的集装箱装运长为5米,底面直径(横截面的外圆直径)为0.1米的圆柱形钢管,你认为采用(2)中的哪种方案在该集装箱中装运钢管数最多?并求出一个这样的集装箱最多能装运多少根钢管?(
 ≈1.73)
≈1.73) 解(1)∵⊙O1、⊙O2、⊙O3两两外切,
∴O1O2=O2O3=O1O3=a
又∵O2A=O3A
∴O1A⊥O2O3
∴O1A=
(2)hn=na,hn′= (n-1)a+a;
(n-1)a+a;
(3)方案二装运钢管最多,
即:按图③的方式排放钢管,放置根数最多,
根据题意,第一层排放31根,第二层排放30根,设钢管的放置层数为n,可得 (n-1)×0.1≤3.1,
(n-1)×0.1≤3.1,
解得n≤35.68,
∵n为正整数,
∴n=35,
钢管放置的最多根数为:31×18+30×17=1068(根)。
∴O1O2=O2O3=O1O3=a
又∵O2A=O3A
∴O1A⊥O2O3
∴O1A=

(2)hn=na,hn′=
 (n-1)a+a;
(n-1)a+a;(3)方案二装运钢管最多,
即:按图③的方式排放钢管,放置根数最多,
根据题意,第一层排放31根,第二层排放30根,设钢管的放置层数为n,可得
 (n-1)×0.1≤3.1,
(n-1)×0.1≤3.1,解得n≤35.68,
∵n为正整数,
∴n=35,
钢管放置的最多根数为:31×18+30×17=1068(根)。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 现有如图①的瓷砖若干块.
现有如图①的瓷砖若干块.
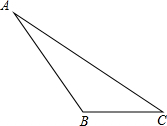
 计算:如图,在△ABC中,DE∥BC,若AD=2,BD=3,AE=1.5,求EC的长.
计算:如图,在△ABC中,DE∥BC,若AD=2,BD=3,AE=1.5,求EC的长.