题目内容
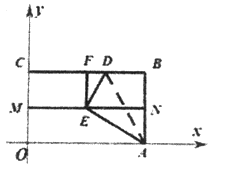
【题目】如图，已知一次函数y1=x+1的图象与y轴交于点A，一次函数y2=kx+b的图象经过点B（0，3），且分别与x轴及y1=x+1的图象交于点C，D，点D的横坐标为
．
（1）求k，b的值；
（2）当x_____时，y2＞0；
（3）若在一次函数y1=x+1的图象上有一点E（
，n），将点E向右平移2个单位后，得对应点E'，判断点E'是否在一次函数y2=kx+b的图象上．
【答案】＜
【解析】试题分析： 
求得点
的坐标，根据点
即可求得
的值.
根据一次函数
求得它与
轴交点坐标，观察图象即可求得.
求得
判断即可.
试题解析：（1）当
时， 
由
可得
解得
．
（2）∵
观察图象可知当
时， 
（3）由题意
时， 
当
时， 
∴点E′不在一次函数
的图象上
练习册系列答案
相关题目
【题目】下表记录了一名球员在罚球线上投篮的结果，
投篮次数（n） | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
投中次数（m） | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
投中频率（n/m） | 0.56 | 0.60 |
| 0.49 |
|
|
（1）计算并填写表中的投中频率（精确到0.01）；
（2）这名球员投篮一次，投中的概率约是多少（精确到0.1）？
【题目】.某区在实施居民用水额定管理前，对居民生活用水情况进行了调查，下表是通过简单随机抽样获得的50个家庭去年月平均用水量
单位：吨
，并将调查数据进行如下整理：
频数分布表
分组 | 划记 | 频数 |
| 正正 | 11 |
|
| 19 |
| ||
合计 |
| 2 50 |
把上面频数分布表和频数分布直方图补充完整；
从直方图中你能得到什么信息？ 
写出两条即可
；
为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按
倍价格收费，若要使
的家庭收费不受影响，你觉得家庭月均用水量应该定为多少？为什么？
