题目内容
13.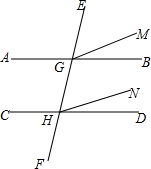 如图,直线AB、CD与EF相交于G、H,且∠EGB=∠EHD.
如图,直线AB、CD与EF相交于G、H,且∠EGB=∠EHD.(1)说明:AB∥CD;
(2)若GM是∠EGB的平分线,HN是∠EHD的平分线,求证:GM∥HN.
分析 (1)根据同位角相等,两直线平行可得AB∥CD;
(2)根据角平分线的定义可得∠EGM=$\frac{1}{2}$∠EGB,∠EHN=$\frac{1}{2}$∠EHD,然后可得∠EGM=∠GHN,再根据同位角相等,两直线平行可得GM∥HN.
解答 证明:(1)∵∠EGB=∠EHD,
∴AB∥CD(同位角相等,两直线平行);
(2)∵GM是∠EGB的平分线,HN是∠EHD的平分线,
∴∠EGM=$\frac{1}{2}$∠EGB,∠EHN=$\frac{1}{2}$∠EHD,
∵∠EGB=∠EHD,
∴∠EGM=∠GHN,
∴GM∥HN.
点评 此题主要考查了平行线的判定,关键是掌握同位角相等,两直线平行.

练习册系列答案
相关题目
3.一个多边形的边数增加1条,则它的内角和增加( )
| A. | 180° | B. | 90° | C. | 360° | D. | 540° |
1. 如图,在数轴上点A表示的数可能是( )
如图,在数轴上点A表示的数可能是( )
 如图,在数轴上点A表示的数可能是( )
如图,在数轴上点A表示的数可能是( )| A. | -3.4 | B. | -2.6 | C. | -1.5 | D. | 2.6 |
5.2014年五一“黄金周”全市接待游客总数为996000人次.将数996000用科学记数法表示应为( )
| A. | 0.996×106 | B. | 96.6×105 | C. | 9.96×105 | D. | 9.96×104 |
2.据报道,肇庆团市委“情系农村”深化农村青年创业小额贷款工作,共发放贷款13 000 000多元,数字13 000 000用科学记数法表示为( )
| A. | 1.3×106 | B. | 1.3×107 | C. | 1.3×108 | D. | 1.3×109 |
 如图,若把太阳看成一个圆,则太阳与地平线l的位置关系是相交(填“相交”、“相切”、“相离”).
如图,若把太阳看成一个圆,则太阳与地平线l的位置关系是相交(填“相交”、“相切”、“相离”).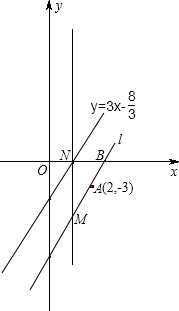 如图,在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线$y=3x-\frac{8}{3}$平行.
如图,在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线$y=3x-\frac{8}{3}$平行.