题目内容
用代入法解下列方程组:
(1)
(2)
(3)
(4)
解:(1)①+②,得8x=6,
x= ,
,
代入①,得y= .
.
则方程组的解为 ;
;
(2)①×2-②,得y= ,
,
代入①,得x-2× =0,
=0,
x= ,
,
则方程组的解为 ;
;
(3)原方程组可化为: ,
,
②×3-①×2,得y=1,
代入①,得3x-5=1,
x=2,
则方程组的解为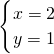 ;
;
(4)原方程组可化为 ,
,
①×7-②,得17x=85,
x=5,
代入①,得15+y=17,
y=2.
则方程组的解为 .
.
分析:根据各个方程组的特点采用相应的方法解答.
点评:这类题目的解题关键是掌握方程组解法中的加减消元法.根据未知数系数的特点,选择合适的方法.
x=
 ,
,代入①,得y=
 .
.则方程组的解为
 ;
;(2)①×2-②,得y=
 ,
,代入①,得x-2×
 =0,
=0,x=
 ,
,则方程组的解为
 ;
;(3)原方程组可化为:
 ,
,②×3-①×2,得y=1,
代入①,得3x-5=1,
x=2,
则方程组的解为
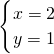 ;
;(4)原方程组可化为
 ,
,①×7-②,得17x=85,
x=5,
代入①,得15+y=17,
y=2.
则方程组的解为
 .
.分析:根据各个方程组的特点采用相应的方法解答.
点评:这类题目的解题关键是掌握方程组解法中的加减消元法.根据未知数系数的特点,选择合适的方法.

练习册系列答案
相关题目