题目内容
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.

【答案】分析:(1)根据OD⊥BC可得出BD= BC=
BC= ,在Rt△BOD中利用勾股定理即可求出OD的长;
,在Rt△BOD中利用勾股定理即可求出OD的长;
(2)连接AB,由△AOB是等腰直角三角形可得出AB的长,再根据D和E是中点可得出DE= ;
;
(3)由BD=x,可知OD= ,由于∠1=∠2,∠3=∠4,所以∠2+∠3=45°,过D作DF⊥OE,DF=
,由于∠1=∠2,∠3=∠4,所以∠2+∠3=45°,过D作DF⊥OE,DF= ,EF=
,EF= x即可得出结论.
x即可得出结论.
解答: 解:(1)如图(1),∵OD⊥BC,
解:(1)如图(1),∵OD⊥BC,
∴BD= BC=
BC= ,
,
∴OD= =
= ;
;
(2)如图(2),存在,DE是不变的.
连接AB,则AB= =2
=2 ,
,
∵D和E分别是线段BC和AC的中点,
∴DE= AB=
AB= ;
;
(3)如图(3),连接OC,
∵BD=x,
∴OD= ,
,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=45°,
过D作DF⊥OE.
∴DF= =
= ,
,
∴在Rt△DEF中,EF= =
= ,
,
∴OE=OF+EF= +
+ =
=
由(2)已知DE= ,
,
∴y= DF•OE=
DF•OE= •
• •
•
= ,(0<x<
,(0<x< ).
).
点评:本题考查的是垂径定理、勾股定理、三角形的性质,综合性较强,难度中等.
 BC=
BC= ,在Rt△BOD中利用勾股定理即可求出OD的长;
,在Rt△BOD中利用勾股定理即可求出OD的长;(2)连接AB,由△AOB是等腰直角三角形可得出AB的长,再根据D和E是中点可得出DE=
 ;
;(3)由BD=x,可知OD=
 ,由于∠1=∠2,∠3=∠4,所以∠2+∠3=45°,过D作DF⊥OE,DF=
,由于∠1=∠2,∠3=∠4,所以∠2+∠3=45°,过D作DF⊥OE,DF= ,EF=
,EF= x即可得出结论.
x即可得出结论.解答:
 解:(1)如图(1),∵OD⊥BC,
解:(1)如图(1),∵OD⊥BC,∴BD=
 BC=
BC= ,
,∴OD=
 =
= ;
;(2)如图(2),存在,DE是不变的.
连接AB,则AB=
 =2
=2 ,
,
∵D和E分别是线段BC和AC的中点,
∴DE=
 AB=
AB= ;
;(3)如图(3),连接OC,
∵BD=x,
∴OD=
 ,
,∵∠1=∠2,∠3=∠4,
∴∠2+∠3=45°,
过D作DF⊥OE.

∴DF=
 =
= ,
,∴在Rt△DEF中,EF=
 =
= ,
,∴OE=OF+EF=
 +
+ =
=
由(2)已知DE=
 ,
,∴y=
 DF•OE=
DF•OE= •
• •
•
=
 ,(0<x<
,(0<x< ).
).点评:本题考查的是垂径定理、勾股定理、三角形的性质,综合性较强,难度中等.

练习册系列答案
相关题目

 如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是
如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是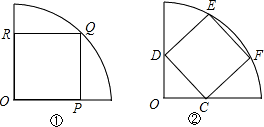

 如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是________平方米(结果中保留π).
如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是________平方米(结果中保留π).