题目内容
9.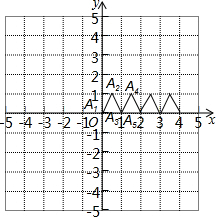 一只电子青蛙在如图的平面直角坐标系做如下运动:从坐标原点开始起跳记为A1,然后沿着边长为1的等边三角形跳跃即A1→A2→A3→A4→A5…已知A3的坐标为(1,0),则A2014的坐标是(1006,$\frac{\sqrt{3}}{2}$).
一只电子青蛙在如图的平面直角坐标系做如下运动:从坐标原点开始起跳记为A1,然后沿着边长为1的等边三角形跳跃即A1→A2→A3→A4→A5…已知A3的坐标为(1,0),则A2014的坐标是(1006,$\frac{\sqrt{3}}{2}$).
分析 根据已知图形得出A2,A4,A6的坐标,进而得出变化规律求出点A2014的坐标.
解答  解:过点A2作A2B,交y轴于点B,
解:过点A2作A2B,交y轴于点B,
由题意可得出:A2B=$\frac{1}{2}$OA3=$\frac{1}{2}$,
∴BO=$\frac{\sqrt{3}}{2}$,
∴A2坐标为:($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
A4坐标为:($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
A6坐标为:($\frac{5}{2}$,$\frac{\sqrt{3}}{2}$),
…
∴点A2014的坐标为(1006,$\frac{\sqrt{3}}{2}$)
故答案是:(1006,$\frac{\sqrt{3}}{2}$).
点评 此题主要考查了等边三角形的性质以及点的坐标变化,得出A2,A4,A6的坐标变化规律是解题关键.

练习册系列答案
相关题目
20.已知x=5是方程x-4+a=3的解,则a的值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
14.如图的四个平面图形中,不是正方体的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列说法不正确的是( )
| A. | 两个有理数的和不一定大于每一个加数 | |
| B. | 任何有理数的绝对值都不小于0 | |
| C. | 最小的非负整数是0 | |
| D. | 一个数的绝对值等于它本身,则这个数是正数. |
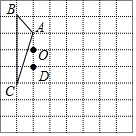 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤: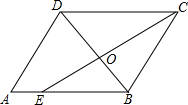 如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O, 已知:如图,AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.
已知:如图,AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH. 如图,长方形的宽为a,用式子表示阴影部分的面积,并计算当a=2时阴影部分的面积.(结果保留π)
如图,长方形的宽为a,用式子表示阴影部分的面积,并计算当a=2时阴影部分的面积.(结果保留π)