题目内容
已知点D、E分别在△ABC的边CA、BA的延长线上,DE∥BC.DE:BC=1:3,设 =
= ,试用向量
,试用向量 表示向量
表示向量 ,
, = .
= .
【答案】分析:首先根据题意画出图形,然后由DE∥BC,可得△ADE∽△ACB,又由DE:BC=1:3,根据相似三角形的对应边成比例,可求得CD=4DA,继而求得答案.
解答: 解:∵DE∥BC,
解:∵DE∥BC,
∴△ADE∽△ACB,
∴DA:CA=DE:BC=1:3,
∵CD=DA+CA,
∴CD=4DA,
∵ =
= ,
,
∴ =-4
=-4 .
.
故答案为:-4 .
.
点评:此题考查了平面向量的知识以及相似三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
解答:
 解:∵DE∥BC,
解:∵DE∥BC,∴△ADE∽△ACB,
∴DA:CA=DE:BC=1:3,
∵CD=DA+CA,
∴CD=4DA,
∵
 =
= ,
,∴
 =-4
=-4 .
.故答案为:-4
 .
.点评:此题考查了平面向量的知识以及相似三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
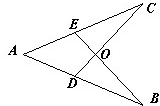 13、如图,已知点D,E分别在线段AB,AC上,BE,CD相交于点O,且AE=AD,添加以下四个条件中的一个,其中不能使△ABE≌△ACD的条件是( )
13、如图,已知点D,E分别在线段AB,AC上,BE,CD相交于点O,且AE=AD,添加以下四个条件中的一个,其中不能使△ABE≌△ACD的条件是( )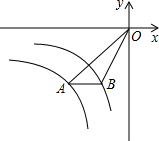 如图,已知点A、B分别在双曲线上
如图,已知点A、B分别在双曲线上 (2013•嘉定区一模)如图,已知点D、E分别在△ABC的边AB和AC上,DE∥BC,AD=
(2013•嘉定区一模)如图,已知点D、E分别在△ABC的边AB和AC上,DE∥BC,AD=