Question

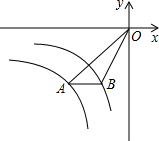如图，已知点A、B分别在双曲线上y=

4

x

（x＜0）和y=

2

x

（x＜0）上，若AB∥x轴，连接OA、OB，则△OAB的面积为

1

．

Answer 1

分析：延长AB交y轴于点C，根据反比例函数系数的几何意义求出△BOC的面积与△AOC的面积，然后相减即可得解．

解答：解：如图，延长AB交y轴于点C，
∵点A、B分别在双曲线上y=

4

x

（x＜0）和y=

2

x

（x＜0）上，且AB∥x轴，
∴S_△BOC=

1

2

×2=1，
S_△AOC=

1

2

×4=2，
∴△OAB的面积=S_△AOC-S_△BOC=2-1=1．
故答案为：1．

点评：本题考查了反比例函数系数的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点，本题作辅助线把△OAB的面积转化为两个三角形的面积的差是解题的关键．