Question

【题目】如图，在□ 中，过点 作 ⊥ 于点 ， ⊥ 于点 ， ．
求证：四边形 是菱形．

Answer 1

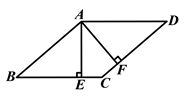
【答案】证明：连接 ，如图．
∵ ⊥ ， ⊥ ， ，

∴ ．
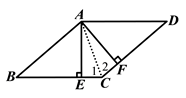
∵四边形 是平行四边形，
∴ ．
∴ ．
∴ ．
∴ ．
∴□ 是菱形．
证法二：
∵四边形 是平行四边形，如图2．
∴ ．
∵ ⊥ ， ⊥ ，
∴ ．

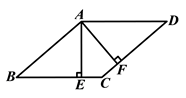
又∵ ，
∴ ≌ ．
∴ ．
∴□ 是菱形．
证法三：
∵四边形 是平行四边形，如图2．
⊥ ， ⊥ ，
∴ ．
∵ ，
∴ ．
∴□ 是菱形．
【解析】方法一：连接AC，由E⊥BC，AF⊥DC，AE=AF，可得∠2=∠1，再由平行线的性质和等腰三角形的判定可证得DA=DC，即可得□ABCD是菱形；方法二：根据已知条件易证△AEB≌△AFD，可得AB=AD，所以□ABCD是菱形；方法三：由平行四边形的面积S=BCAE=CDAF，即可证得BC=CD，所以□ABCD是菱形．
【考点精析】通过灵活运用等腰三角形的判定和平行四边形的性质，掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分即可以解答此题．