Question

如图，A、B是双曲线y=

k

x

(k＞0)上的点，A、B两点的横坐标分别是a、3a，线段AB的延长线交x轴于点C，若S_△AOC=6，则k的值为（　　）

A．2

B．3

C．4

D．6

Answer 1

分析：分别过点A、B作AF⊥y轴于点F，AD⊥x轴于点D，BG⊥y轴于点G，BE⊥x轴于点E，由于反比例函数的图象在第二象限，所以k＜0，由点A是反比例函数图象上的点可知，S_△AOD=S_△AOF=

|k|

2

，再由A、B两点的横坐标分别是a、3a可知AD=3BE，故点B是AC的三等分点，故DE=2a，CE=a，所以S_△AOC=S_梯形ACOF-S_△AOF=6，故可得出k的值．

解答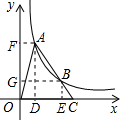：解：分别过点A、B作AF⊥y轴于点F，AD⊥x轴于点D，BG⊥y轴于点G，BE⊥x轴于点E，
∵k＞0，点A是反比例函数图象上的点，
∴S_△AOD=S_△AOF=

|k|

2

，
∵A、B两点的横坐标分别是a、3a，
∴AD=3BE，
∴点B是AC的三等分点，
∴DE=2a，CE=a，
∴S_△AOC=S_梯形ACOF-S_△AOF=

1

2

（OE+CE+AF）×OF-

|k|

2

=

1

2

×5a×

|k|

a

-

|k|

2

=6，解得k=3．
故选B．

点评：本题考查的是反比例函数系数k的几何意义，根据题意得出辅助线得出S_△AOC=S_梯形ACOF-S_△AOF=6是解答此题的关键．