题目内容
3.若关于x的方程(3+a)x2-5x+1=0有实数根,则整数a的最大值3.分析 由于关于x的方程(3+a)x2-5x+1=0有实数根,分情况讨论:
①当3+a=0即a=-3时,此时方程为一元一次方程,方程一定有实数根;
②当3+a≠0即a≠-3时,此时方程为一元二次方程,如果方程有实数根,那么其判别式是一个非负数,由此可以确定整数a的最大值.
解答 解:当a=-3时,原方程可化为-5x+1=0,解得:x=$\frac{1}{5}$,此时方程有实数根;
当a≠-3时,∵关于x的方程(3+a)x2-5x+1=0有实数根,
∴△=(-5)2-4×(3+a)×1≥0,即13-4a≥0,
解得:a≤$\frac{13}{4}$,
则整数a的最大值为3,
故答案为:3.
点评 本题考查了一元二次方程根的判别式的应用.一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
注意此方程应分是一元二次方程与不是一元二次方程两种情况进行讨论.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
14.下列各数中无理数是( )
| A. | $\frac{π}{2}$ | B. | $\frac{22}{7}$ | C. | $\sqrt{4}$ | D. | $\root{3}{27}$ |
18. 一次函数y=kx+b(k≠0,k与b都是常数)图象如图示,当y<2时,变量x的取值范围是( )
一次函数y=kx+b(k≠0,k与b都是常数)图象如图示,当y<2时,变量x的取值范围是( )
 一次函数y=kx+b(k≠0,k与b都是常数)图象如图示,当y<2时,变量x的取值范围是( )
一次函数y=kx+b(k≠0,k与b都是常数)图象如图示,当y<2时,变量x的取值范围是( )| A. | x>0 | B. | x<0 | C. | x<2 | D. | x>2 |
8.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (1+a)(a-1)=a2-1 | C. | a2+ab+b2=(a+b)2 | D. | (x+3)2=x2+3x+9 |
 如图,直线y=$\frac{4}{3}$x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$.
如图,直线y=$\frac{4}{3}$x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$.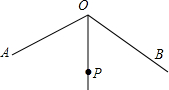 如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( ) 已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,且与双曲线y=$\frac{k}{x}$交于点C(1,a).
已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,且与双曲线y=$\frac{k}{x}$交于点C(1,a).