题目内容
已知抛物线的解析式y=ax2+c满足如下三个条件:a+c=3,ac=-4,a<c.
(1)求这条抛物线的解析式;
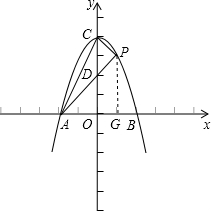
(2)设该抛物线与x轴的两个交点分别为A、B(A在B的左边),与y轴的交点为C.
①在第一象限内,这条抛物线上有一点P,AP交y轴于点D,若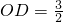 ,试比较S△APC与S△AOC的大小;
,试比较S△APC与S△AOC的大小;
②在第一象限内,这条抛物线上是否存在点P′,使得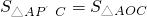 ?若存在,请求出点P′的坐标;若不存在,请说明理由.
?若存在,请求出点P′的坐标;若不存在,请说明理由.
 解:(1)由
解:(1)由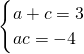
解得:
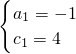 或
或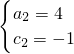 ,
,∵a<c,
∴
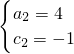 (不合题意,舍去),
(不合题意,舍去),∴a=-1,c=4,
∴所求的抛物线的解析式为:y=-x2+4;
(2)①在抛物线y=-x2+4中,令y=0,
得x=±2;
当x=0时,y=4,
∴A、B、C三点的坐标分别为(-2,0),(2,0),(0,4).
过点P作PG⊥x轴于G,设点P的坐标为(m,n),
∵点P在抛物线y=-x2+4上的第一象限内的点,
∴m>0,n>0,且n=-m2+4,
∴PG=-m2+4,OA=2,AG=m+2,
∵OD∥PG,OD=
 ,
,∴
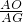 =
=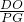 ,
,即
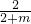 =
=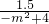 ,
,解得m1=
 ,m2=-2(舍去),
,m2=-2(舍去),∴OG=
 .
.又∵CD=OC-OD=4-1.5=2.5,
∴S△PDC=
 CD•GO=
CD•GO= ×
× ×
× =
= ,
,∴S△AOD=
 AO•DO=
AO•DO= ×2×
×2× =
=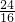 ,
,∴S△PDC>S△AOD.
又∵S△APC=S△PDC+S△ADC,S△AOC=SAOD+SADC,
∴S△APC>S△AOC,
②在第一象限内,设在抛物线上存在点P′(m,n),
使得
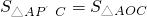 ,
,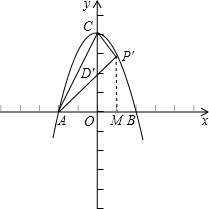
过点P′作P′M⊥x 轴于点M,
则m>0,n>0且n=-m2+4.
∴OM=m,P′M=-m2+4,OA=2,AM=m+2,
设AP′交y轴于点D′,设OD′=t,
∵OD′∥P′M,
∴
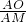 =
=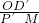 ,即
,即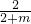 =
=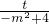 ,
,化简得mt+2t=8-m2 ①
∵CD′=OC-OD′=4-t,
∴S△P′CD′=
 CD′•OM=
CD′•OM= (4-t)•m,
(4-t)•m,S△AOD′=
 OA•OD′=
OA•OD′= ×2•t=t,
×2•t=t,∵
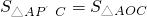 ,
,∴
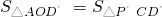 ,
,即t=
 (4-t)m,即mt+2t=4m ②
(4-t)m,即mt+2t=4m ②由①②两式得8-2m2=4m,
即m2+2m-4=0,
解得:m1=
 -1,m2=-
-1,m2=- -1(不合题意舍去),
-1(不合题意舍去),此时,
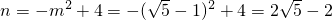 .
.∴存在点P′(
 -1,2
-1,2 -2),
-2),使得
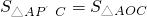 .
.分析:(1)将a+c=3,ac=-4组合,利用a<c,即可确定a,c的值;
(2)①利用点P在抛物线y=-x2+4上的第一象限内的点,得出m>0,n>0,且n=-m2+4,进而求出OG=
 ,再利用已知求出S△PDC,S△AOD的面积,进而得出S△APC与S△AOC的大小关系;
,再利用已知求出S△PDC,S△AOD的面积,进而得出S△APC与S△AOC的大小关系;(2)利用平行线分线段成比例定理得出
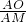 =
=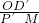 ,以及利用三角形面积关系得出
,以及利用三角形面积关系得出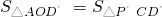 ,进而求出m的值,即可求出点P′的坐标.
,进而求出m的值,即可求出点P′的坐标.点评:此题主要考查了二次函数的综合应用以及一元二次方程解法和三角形面积求法等知识,熟练利用三角形面积关系得出是解题关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目