题目内容
2.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
分析 求出∠CDA=∠ACB=90°,根据有两个角对应相等的两三角形相似得出△ACD∽△CBD,即可得出答案.
解答 解:∵∠ACB=90°,CD⊥AB,
∴∠CDA=∠CDB=90°,
∵∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
故选:C.
点评 本题考查了相似三角形的判定,直角三角形的性质,熟练掌握相似三角形的判定是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
7. 为有效保护日益减少的水资源,某市提倡居民节约用水,并对该市居民用水采取分段收费:每户每月用水不超过20m3,每立方米收费3元;若用水超过20m3,超过部分每立方米收费5元.该市某居民家8月份交水费84元,则该居民家8月份用水量为多少m3?如果设该居民家8月份用水量为xm3,则下面所列方程中正确的是( )
为有效保护日益减少的水资源,某市提倡居民节约用水,并对该市居民用水采取分段收费:每户每月用水不超过20m3,每立方米收费3元;若用水超过20m3,超过部分每立方米收费5元.该市某居民家8月份交水费84元,则该居民家8月份用水量为多少m3?如果设该居民家8月份用水量为xm3,则下面所列方程中正确的是( )
 为有效保护日益减少的水资源,某市提倡居民节约用水,并对该市居民用水采取分段收费:每户每月用水不超过20m3,每立方米收费3元;若用水超过20m3,超过部分每立方米收费5元.该市某居民家8月份交水费84元,则该居民家8月份用水量为多少m3?如果设该居民家8月份用水量为xm3,则下面所列方程中正确的是( )
为有效保护日益减少的水资源,某市提倡居民节约用水,并对该市居民用水采取分段收费:每户每月用水不超过20m3,每立方米收费3元;若用水超过20m3,超过部分每立方米收费5元.该市某居民家8月份交水费84元,则该居民家8月份用水量为多少m3?如果设该居民家8月份用水量为xm3,则下面所列方程中正确的是( )| A. | 3x+5=84 | B. | 3×20+5x=84 | C. | 3×20+5(x-20)=84 | D. | 3x+5(x-20)=84 |
14.2016年,在复杂的国际形势下,我国在经济方面仍然取得了骄人的成绩,2017年1月20日,国家统计局公布:2016年中国国内生产总值GDP达744127亿元,同比增长6.7%.数据744127亿元用科学记数法表示为( )
| A. | 74.4127×1011元 | B. | 74.4127×1012元 | C. | 7.44127×1013元 | D. | 7.44127×1014元 |
11.不等式-2x<6变形为x>-3的依据是( )
| A. | 不等式的性质1 | B. | 不等式的性质2 | C. | 不等式的性质3 | D. | 等式的基本性质2 |
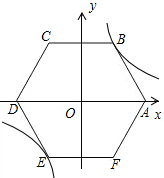 如图,在平面直角坐标系中,正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=$\frac{9\sqrt{3}}{x}$位于第一象限的图象上,则正六边形ABCDEF的边长为6.
如图,在平面直角坐标系中,正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=$\frac{9\sqrt{3}}{x}$位于第一象限的图象上,则正六边形ABCDEF的边长为6.