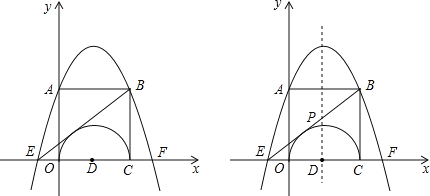Question

【题目】设抛物线F的解析式为：y＝2x2﹣4nx+2n2+n，n为实数．

（1）求抛物线F顶点的坐标（用n表示），并证明：当n变化时顶点在一条定直线l上；

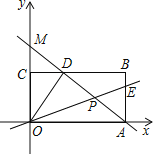
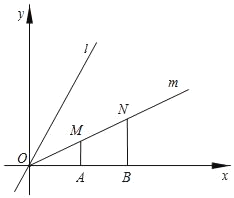
（2）如图，射线m是（1）中直线l与x轴正半轴夹角的平分线，点M，N都在射线m上，作MA⊥x轴、NB⊥x轴，垂足分别为点A、点B（点A在点B左侧），当MA+NB＝MN时，试判断是否为定值，若是，请求出定值；若不是，说明理由．

（3）已知直线y＝kx+b与抛物线F中任意一条都相截，且截得的长度都为，求这条直线的解析式．

Answer 1

【答案】（1）详见解析；（2）2；（3）y＝x+2．

【解析】

（1）将抛物线配方成顶点式可得顶点坐标及其所在直线解析式；
（2）由直线l的斜率及角平分线得出∠NOB=30°、MA=OM、NB=ON，根据MA+NB=OM+ON=OM+（OM+MN）=MN知OM=MN，由可得答案；
（3）联立得2x2-（4n+k）x+2n2+n-b=0，设交点坐标为P（x1、y1）、Q（x2，y2），由韦达定理知x1+x2=、x1x2=，从而由为定值得k=，进一步求解可得．

（1）∵y＝2x2﹣4nx+2n2+n＝2（x﹣n）2+n，

∴抛物线的顶点坐标为F（n， n），

由图可设直线l的解析式为y＝kx，

将点F（n， n）代入，得： n＝kn，

解得：k＝，

则当n变化时，顶点在直线y＝x上；

（2）∵由直线l的斜率为知直线l与x轴正半轴的夹角为60°，

∴∠NOB＝30°，MA＝OM、NB＝ON，

MA+NB＝OM+ON＝OM+（OM+MN）＝MN，

∴OM＝MN，

则＝2；

（3）联立，得：2x2﹣（4n+k）x+2n2+n﹣b＝0，

设交点坐标为P（x1、y1）、Q（x2，y2），

由韦达定理知x1+x2=、x1x2=，

∴PQ＝

＝

＝

＝为定值，

则一定有k＝，

代入得3+8b＝19，

解得b＝2，

故直线的解析式为y＝x+2．