题目内容
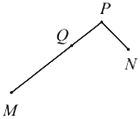
【题目】如图,数轴上点![]() ,
,![]() 表示的数
表示的数![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),
重合),![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 同时向数轴正方向移动,点
同时向数轴正方向移动,点![]() 运动速度为每秒2个单位长度,点
运动速度为每秒2个单位长度,点![]() 运动速度为每秒3个单位长度,设运动时间为
运动速度为每秒3个单位长度,设运动时间为![]() 秒(
秒(![]() ).
).
(1)直接写出![]() ______,
______,![]() ______;
______;
(2)若![]() 点表示的数是0.
点表示的数是0.
①![]() ,则
,则![]() 的长为______(直接写出结果);
的长为______(直接写出结果);
②点![]() ,
,![]() 在移动过程中,线段
在移动过程中,线段![]() ,
,![]() 之间是否存在某种确定的数量关系,判断并说明理由;
之间是否存在某种确定的数量关系,判断并说明理由;
(3)点![]() ,
,![]() 均在线段
均在线段![]() 上移动,若
上移动,若![]() ,且
,且![]() 到线段
到线段![]() 的中点
的中点![]() 的距离为3,请求出符合条件的点
的距离为3,请求出符合条件的点![]() 表示的数.
表示的数.
【答案】(1)![]() ,
,![]() ;(2)①5;②
;(2)①5;②![]() ,理由详见解析;(3)符合条件的点
,理由详见解析;(3)符合条件的点![]() 表示的数为-2,0,或-4.
表示的数为-2,0,或-4.
【解析】
(1)根据非负数的性质得出a、b的值即可;
(2)①根据路程=速度×时间得到N、M表示的数,再根据两点间的距离公式即可求解;
②分别表示出AN、PM,进一步得到线段BM、MN之间的数量关系式;
(3)设点![]() 表示的数为
表示的数为![]() ,则点
,则点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,得到
,得到![]() ,得出
,得出![]() 或
或![]() ,根据条件得到点
,根据条件得到点![]() 表示的数为0或6,得到
表示的数为0或6,得到![]() 或
或![]() 解出t的值代入
解出t的值代入![]() 和
和![]() ,求出x的值即可.
,求出x的值即可.
(1)∵|a+6|+(b-12)2=0,且|a+6|≥0,(b-12)2≥0,
∴a+6=0,b-12=0,
解得,![]() ,
,![]() ;
;
(2)①运动1秒后,N表示的数:0-3×1=-3;M表示的数:0+2×1=2;
∴MN=2-(-3)=5.
故答案为:5;
②![]() ,理由如下:
,理由如下:
依题意![]() ,
,![]() ,
,
ⅰ当![]() 在
在![]() 的左边时,如图1,
的左边时,如图1,
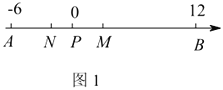
∴![]() ,
,![]() ,
,
∴![]() ;
;
ⅱ当![]() 在
在![]() 的右边时,如图2,
的右边时,如图2,
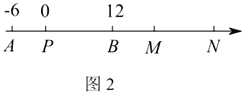
∴![]() ,
,![]() ,
,
∴![]() ,
,
综上所述,点![]() ,
,![]() 在移动过程中,线段
在移动过程中,线段![]() ;
;
(3)设点![]() 表示的数为
表示的数为![]() ,
,
则点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,
,
依题意![]() ,
,
即![]() ,
,![]() ,
,
![]() 或
或![]() ,
,
∵![]() 为线段
为线段![]() 的中点,
的中点,![]() 点表示的数为3,
点表示的数为3,
即![]() ,点
,点![]() 表示的数为0或6,
表示的数为0或6,
∴![]() 或
或![]() ,
,
![]() 或4,
或4,
①当![]() 时,
时,
由![]() 得
得![]() ;
;
由![]() 得
得![]() (此时与点
(此时与点![]() 重合,不符合题意,舍去);
重合,不符合题意,舍去);
②当![]() 时,
时,
由![]() 得
得![]() ;
;
由![]() 得
得![]() .
.
综上所述,符合条件的点![]() 表示的数为-2,0,或-4.
表示的数为-2,0,或-4.
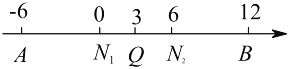

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案